
Estava agora praticando o cálculo de áreas com integrais.
Gostava de saber como tirar os pontos necessários. Igualo as expressões?
Cumprimentos!



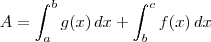





john escreveu:Estive a tentar e fiquei só com uma dúvida. Existe uma ordem específica para os valores dos integrais?
 .
.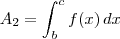 .
. .
.


john escreveu:Mas a parte dos valores não percebi. Porquê b em cima e a em baixo e c em cima e b em baixo? Não poderia ser assim?
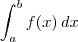 significa que você está integrando a função f partindo de a e indo para b. Ou seja, o intervalo de integração começa no valor que fica abaixo do símbolo de integral (nesse caso a) e termina no valor que está acima do símbolo (nesse caso b).
significa que você está integrando a função f partindo de a e indo para b. Ou seja, o intervalo de integração começa no valor que fica abaixo do símbolo de integral (nesse caso a) e termina no valor que está acima do símbolo (nesse caso b).



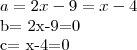
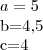


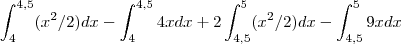
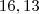

 .
. .
.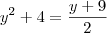
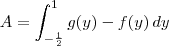

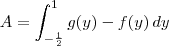

john escreveu:No exercício anterior era a somar. Porque é que neste é a subtrair?


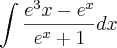


 . (Vou lembrar-lhe novamente: Cuidado com a notação!)
. (Vou lembrar-lhe novamente: Cuidado com a notação!)
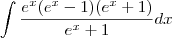
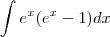
 .
.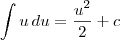
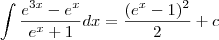


LuizAquino escreveu:Primeiro, você deve notar que o sistema de eixos está "trocado". O que geralmente chamamos de x é agora y e o que geralmente chamamos de y agora é x. Arrumando a figura, ficamos com a ilustração abaixo.
Estamos vendo x como a variável dependente e y como a variável independente.
A função representando a parábola é (basta isolar x na expressão dada):.
Já a função representando a reta é (basta isolar x na expressão dada):.
Agora, você precisar determinar as interseções entre a parábola e a reta, isto é, calcular as soluções da equação f(y)=g(y):
Resolvendo essa equação, você obtemos y=1 e y=-1/2.
Portanto, a área procurada é dada pela integral:
Resolvendo essa integral, você irá encontrar A=9/16.
Esse é um típico exercício de Cálculo para testar se o aluno consegue trabalhar com diferentes sistemas de eixos.
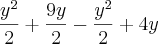

john escreveu:
Fiz a integral e deu-me:
Substituindo não me dá 9/6 :s
 , com n diferente de -1.
, com n diferente de -1.

john escreveu:Sinceramente não percebi onde errei. Pode-me ajudar? O n é diferente de -1.
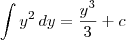 .
.
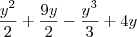 ?
?
john escreveu:Então fica:?
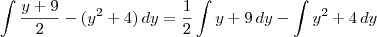


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)