Olá Amigos!
Tudo bem?
Estou entrando em contato porque eu fiz essa derivada, e não está batendo com gabarito de resposta, gostaria que em ajudasse a resolver e me mostrasse aonde estou errando por favor.
mais antes veja o que fiz
u=tg(x)
du=sec²(x)dx
?tg³(x)sec²(x)dx=
?u³du=
(u^3)/3+c=
tg^3(x)/3
3x2.34
?
não consigo entender aonde to errando?
se pode me ajudar por favor.
Não posso criar novos tópicos, não entendi motivo mesmo
gostaria de resposta sobre isso..
e para evitar problemas, tirei questão em anexo.
vou escrever.
? (3 sec x tgx - 5 cos sec^2 x) dx
Bom tah ai!
se pode me ajudar me orientando, não fazendo para "mim" eu agradeço!


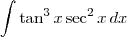
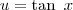 . Desse modo,
. Desse modo, 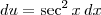 . Portanto, temos que
. Portanto, temos que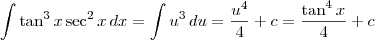
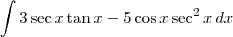
 , então essa integral é o mesmo que:
, então essa integral é o mesmo que: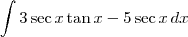
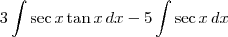
 .
. . Ou seja, teremos:
. Ou seja, teremos: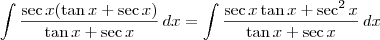
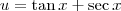 , temos que
, temos que 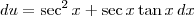 . Portanto, ficamos:
. Portanto, ficamos: .
.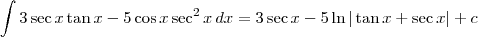


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)