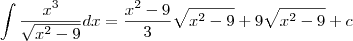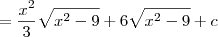por Manoella » Ter Fev 08, 2011 23:47
por Manoella » Ter Fev 08, 2011 23:47
Ajude me a decifrar essa integral:
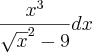
Se alguém puder me ajudar ficarei grata.
-
Manoella
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Dez 16, 2010 09:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Santa Lucci » Qua Fev 09, 2011 00:23
por Santa Lucci » Qua Fev 09, 2011 00:23
Olá, tudo bom?
Bom, comecei a fazer aqui... Não terminei por dar muito trabalho (mesmo).
Fiz assim: substitui x^(1/2) por u, depois faz uma integração por fração parcial...
Mas, desisti.
Onde achou essa integral?
Att,
Santa Lucci.
-
Santa Lucci
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jan 02, 2011 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
 por LuizAquino » Qua Fev 09, 2011 09:13
por LuizAquino » Qua Fev 09, 2011 09:13
Manoella escreveu:Ajude me a decifrar essa integral:
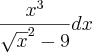
Se alguém puder me ajudar ficarei grata.
Pelo que você escreveu, a integral desejada é:
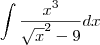
Considerando x positivo, temos que
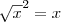
. Sendo assim, essa integral é a mesma que:
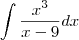
Como no numerador temos um polinômio de grau maior do que o do denominador, então efetuamos a divisão entre esses polinômios, obtendo que o quociente será
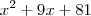
e o resto será 729, ou seja,
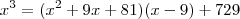
. Desse modo, temos que:
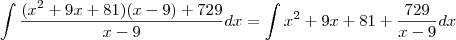
De onde obtemos que:
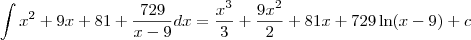
, com c uma constante.
ObservaçãoSe essa não era a integral que você queria, então por favor digite a integral desejada de forma
correta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Manoella » Qua Fev 09, 2011 09:44
por Manoella » Qua Fev 09, 2011 09:44
Realmente cometi um serio erro ao digitar, na realidade a integral que quero é essa. Desculpas pela falha;
![\frac{x^3}{\sqrt[]{x^2-9}}dx \frac{x^3}{\sqrt[]{x^2-9}}dx](/latexrender/pictures/f6d1b2f92b7c91e6cc34322189876a98.png)
Desde de já meu pedido de desculpas e meu agradecimento pela colaboração.
-
Manoella
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Dez 16, 2010 09:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Qua Fev 09, 2011 10:09
por LuizAquino » Qua Fev 09, 2011 10:09
Manoella escreveu:Realmente cometi um serio erro ao digitar, na realidade a integral que quero é essa. Desculpas pela falha;
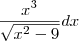
Tudo bem, mas nas próximas vezes tenha mais cuidado com a escrita. Em Matemática (assim como em Português) um símbolo fora do lugar muda completamente o sentido do que está escrito.
Pois bem, vejamos a solução da integral:
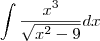
Fazendo por substituição, temos que se
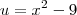
, então

. Desse modo, obtemos:
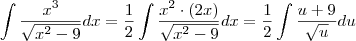
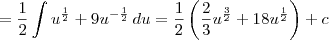
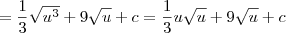
, onde c é uma constante.
Desfazendo a substituição, obtemos:
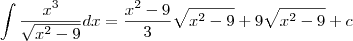
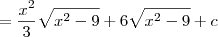
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4612 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4581 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4343 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2866 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
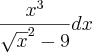


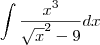
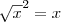 . Sendo assim, essa integral é a mesma que:
. Sendo assim, essa integral é a mesma que: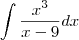
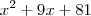 e o resto será 729, ou seja,
e o resto será 729, ou seja, 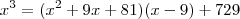 . Desse modo, temos que:
. Desse modo, temos que: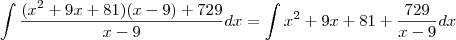
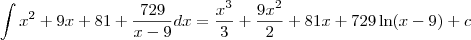 , com c uma constante.
, com c uma constante.
![\frac{x^3}{\sqrt[]{x^2-9}}dx \frac{x^3}{\sqrt[]{x^2-9}}dx](/latexrender/pictures/f6d1b2f92b7c91e6cc34322189876a98.png)

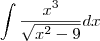
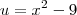 , então
, então  . Desse modo, obtemos:
. Desse modo, obtemos: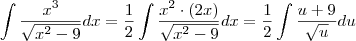
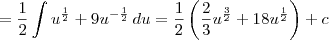
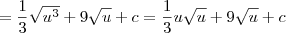 , onde c é uma constante.
, onde c é uma constante.