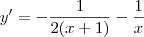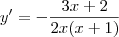por Moura » Sex Jan 14, 2011 12:16
por Moura » Sex Jan 14, 2011 12:16
Determine as derivadas de y em relação a x:
1)
![y=ln\frac{1}{x.\sqrt[]{x+1}} y=ln\frac{1}{x.\sqrt[]{x+1}}](/latexrender/pictures/746dfa3c7d00e8f4583cee065a5ea0a9.png)
Resp.:
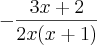
2)

Resp.:

Desde de já agradeço.

P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Elcioschin » Sex Jan 14, 2011 14:12
por Elcioschin » Sex Jan 14, 2011 14:12
Vou fazer a primeira para você aprender:
Lembre-se que Dx lnu = (1/u)*Dx(u)
No teu caso u = 1/x*V(x + 1) = 1/x*(x + 1)^(1/2) ----> 1/u = x*V(x + 1) = x*(x + 1)^(1/2)
Dx(u) = Dx[1/x*V(x + 1)] ---> Dx(u) = Dx[x*(-1)*(x + 1)^(-1/2)] ----> Dx(u) = x^(-1)*[(-1/2)*(x + 1)^(-3/2] + (x + 1)^(-1/2)*[-1*x^(-2)]
Dx(u) = - 1/2*x*(x + 1)^(3/2) - 1/x²*(x + 1)^(1/2)
y' = [x*(x + 1)^(1/2)]*[- 1/2*x*(x + 1)^(3/2) - 1/x²*(x + 1)^(1/2)]
y' = - 1/2*(x + 1) - 1/x
y' = - (3x + 2)/2*x*(x + 1)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Moura » Sex Jan 14, 2011 15:13
por Moura » Sex Jan 14, 2011 15:13
Agradeço a ajuda mais não consigo entender dessa maneira, poderia, por favor, escrever com formula matemática usando o editor.
Obrigado.
P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Moura » Sex Jan 14, 2011 16:00
por Moura » Sex Jan 14, 2011 16:00
Editado pela última vez por
Moura em Sex Jan 14, 2011 21:26, em um total de 1 vez.
P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Elcioschin » Sex Jan 14, 2011 18:05
por Elcioschin » Sex Jan 14, 2011 18:05
Moura
Agradeço a sua excelente ajuda. Ficou mais fácil visualizar.
Há necessidade apenas de uma pequena correção, na 5ª linha
a) Colocar um colchete logo após x^(-3/2)]
b) Corrigir o final: [(-1)*x^(-2)]
Infelizmente eu não tenho poderes para editar sua mensagem. Por isto solicito a você o obséquio da fazê-lo.
E agradeço novamente
Elcio
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5031 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6661 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2261 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7472 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4939 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y=ln\frac{1}{x.\sqrt[]{x+1}} y=ln\frac{1}{x.\sqrt[]{x+1}}](/latexrender/pictures/746dfa3c7d00e8f4583cee065a5ea0a9.png)
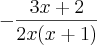




![y=ln\frac{1}{x.\sqrt[]{x+1}} y=ln\frac{1}{x.\sqrt[]{x+1}}](/latexrender/pictures/746dfa3c7d00e8f4583cee065a5ea0a9.png)
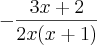







![u=\frac{1}{x.\sqrt[]{x+1}}=\frac{1}{x(x+1){}^{1/2}}\rightarrow\frac{1}{u}=x.\sqrt[]{x+1}=x(x+1){}^{\frac{1}{2}} u=\frac{1}{x.\sqrt[]{x+1}}=\frac{1}{x(x+1){}^{1/2}}\rightarrow\frac{1}{u}=x.\sqrt[]{x+1}=x(x+1){}^{\frac{1}{2}}](/latexrender/pictures/d0ce65623421cf815bf4ae5663709471.png)
![Dx(u)=Dx(\frac{1}{x.\sqrt[]{x+1}}) Dx(u)=Dx(\frac{1}{x.\sqrt[]{x+1}})](/latexrender/pictures/e2f2dabc6d59968ee1a2c057ebf9c897.png)
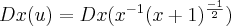

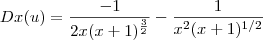
^\frac{3}{2}}-\frac{1}{x^2(x+1)^{1/2}}) y'=[x(x+1)^{\frac{1}{2}}](\frac{-1}{2x(x+1)^\frac{3}{2}}-\frac{1}{x^2(x+1)^{1/2}})](/latexrender/pictures/fd2b1e4bbe36c9813e9d6931b3079fa1.png)