![\int_{1}^{4}\sqrt[]{xdx} \int_{1}^{4}\sqrt[]{xdx}](/latexrender/pictures/985c348818a9b39ac15aaa44332766fd.png) , com n=6 PELA REGRA DE SIMPSON? CONSIDERE 4 CASAS DECIMAIS.
, com n=6 PELA REGRA DE SIMPSON? CONSIDERE 4 CASAS DECIMAIS.RESPOSTA: 4,6678

![\int_{1}^{4}\sqrt[]{xdx} \int_{1}^{4}\sqrt[]{xdx}](/latexrender/pictures/985c348818a9b39ac15aaa44332766fd.png) , com n=6 PELA REGRA DE SIMPSON? CONSIDERE 4 CASAS DECIMAIS.
, com n=6 PELA REGRA DE SIMPSON? CONSIDERE 4 CASAS DECIMAIS.
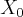 ,
,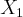 ,
,  .
. , QUE DEVERÃO ESTAR IGUALMENTEESPAÇADOS. CHEGANDO A SEGUINTE FÓRMULA:
, QUE DEVERÃO ESTAR IGUALMENTEESPAÇADOS. CHEGANDO A SEGUINTE FÓRMULA: .[
.[ +
+ +
+ +
+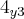 +
+ +...+
+...+ +
+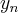 ].
].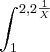 dx COM N= 6.
dx COM N= 6.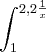 dx= 1ntal que x
dx= 1ntal que x 
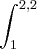 = 1n tal que 2,2 tal que - 1n tal que 1 talque= 0,7885 - 0 = 0,7885
= 1n tal que 2,2 tal que - 1n tal que 1 talque= 0,7885 - 0 = 0,7885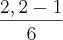 )=0,2
)=0,2





Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)