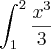por Anakinrj » Ter Nov 23, 2010 21:33
por Anakinrj » Ter Nov 23, 2010 21:33

Bom estou com uma duvida sobre essa questao.
Calcular essa integral
1
? x²dx= com a seguinte resposta 7/3 u.d.s
2
Como se faz?

-
Anakinrj
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 23, 2010 21:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por VtinxD » Qua Nov 24, 2010 01:51
por VtinxD » Qua Nov 24, 2010 01:51
Faça pelo Teorema fundamental do cálculo, porem perceba que não existe área negativa.
Mesmo assim ,particularmente, acho estranho a resposta não ser negativa, que é a resolução pelo teorema fundamental do cálculo e não sua interpretação geométrica.
Espero ter ajudado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por Anakinrj » Qua Nov 24, 2010 11:55
por Anakinrj » Qua Nov 24, 2010 11:55
So mais uma duvida o que significa u.d.s?
-
Anakinrj
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 23, 2010 21:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Neperiano » Qua Nov 24, 2010 12:10
por Neperiano » Qua Nov 24, 2010 12:10
Ola
Deve ser Unidade de ... dai eu não sei, segmento talvez o certo seria u.a, mas pode ser assim tmb
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Jefferson » Sáb Nov 27, 2010 23:02
por Jefferson » Sáb Nov 27, 2010 23:02
Depende do contexto se faz referência com área:
U d s = Unidade de Superfície mais comum usar U A = Unidade de área.
Na verdade toda vez que não foi definida uma unidade padrão o ideal é calcular o valor numérico,
sem unidade. E não sair criando uma unidade para o que não tem.
-
Jefferson
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 16, 2010 23:18
- Localização: Vila Velha - ES
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Dom Nov 28, 2010 00:07
por MarceloFantini » Dom Nov 28, 2010 00:07
Na verdade usar
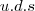
ou

está certo, pois não está criando uma nova unidade, apenas deixando a unidade livre.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por andrefahl » Dom Nov 28, 2010 00:11
por andrefahl » Dom Nov 28, 2010 00:11
u.d.s para unidades de segmento...
para uma integral que naum é d linha....
=P
eu mereços essas coisas viu!
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por demolot » Sáb Dez 11, 2010 14:13
por demolot » Sáb Dez 11, 2010 14:13
Basta primitivar e aplicar o integral
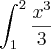
Substituis 1º por 1 e subtrais por substituição de 2
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
 por Moura » Ter Dez 14, 2010 06:58
por Moura » Ter Dez 14, 2010 06:58
P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular área
por Anakinrj » Qua Nov 24, 2010 12:11
- 2 Respostas
- 2287 Exibições
- Última mensagem por Moura

Ter Dez 14, 2010 07:44
Cálculo: Limites, Derivadas e Integrais
-
- Calcular área
por pedcoi » Qui Fev 02, 2012 11:19
- 2 Respostas
- 2043 Exibições
- Última mensagem por pedcoi

Sex Fev 03, 2012 14:03
Cálculo: Limites, Derivadas e Integrais
-
- Calcular unidades de área?
por natanlp » Qua Fev 01, 2012 00:45
- 9 Respostas
- 5690 Exibições
- Última mensagem por Arkanus Darondra

Qua Fev 01, 2012 15:34
Geometria Analítica
-
- [INTEGRAL]Calcular área y=x^2
 por krtc » Qua Jul 24, 2013 02:07
por krtc » Qua Jul 24, 2013 02:07
- 5 Respostas
- 3714 Exibições
- Última mensagem por Russman

Qua Jul 24, 2013 03:13
Cálculo: Limites, Derivadas e Integrais
-
- calcular a área da funçao
 por edilaine33 » Dom Dez 01, 2013 08:54
por edilaine33 » Dom Dez 01, 2013 08:54
- 1 Respostas
- 1696 Exibições
- Última mensagem por Pessoa Estranha

Dom Dez 01, 2013 10:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Bom estou com uma duvida sobre essa questao.
Bom estou com uma duvida sobre essa questao.

 Bom estou com uma duvida sobre essa questao.
Bom estou com uma duvida sobre essa questao.





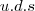 ou
ou  está certo, pois não está criando uma nova unidade, apenas deixando a unidade livre.
está certo, pois não está criando uma nova unidade, apenas deixando a unidade livre.