 por Thiagom » Ter Nov 02, 2010 17:54
por Thiagom » Ter Nov 02, 2010 17:54
Uma das coisas que mais me da raiva no ensino superior publico do brasil eh que: o aluno eh que tem que se virar pra aprender, pois professor so ensina o basicão e quando voce se depara com algo mais avançado voce fica todo bolado...
Enfim, meu professor de calculo passou um trabalho que eu to penando pra fazer, e tou vindo aqui como ultimo recurso antes deu desistir de novo dessa cadeira...
O limite eh o seguinte
![\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[2]{x-1}-1} \lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[2]{x-1}-1}](/latexrender/pictures/1a995369b61d86c46d174fe2c5af639c.png)
tentei multiplicar pelos conjugados, mas da sempre indeterminação, depois tenti multiplicar usando a formula dos cubos, mas mesmo assim anda da indeterminação no numerador... eu não sei mais o que fazer.... a ficha da como resultado: 5/6
Desculpem raiva, mas esse limite realmente me conseguiu tirar do sério...
-
Thiagom
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 02, 2010 17:36
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Ter Nov 02, 2010 18:16
por Neperiano » Ter Nov 02, 2010 18:16
Ola
Tem uma regra que se chama regra de L'hopital, quando de 0 emcima e 0 embaixo, voce deriva emcima e embaixo separadamente, talvez tenha que usar ela, tente uma vez.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Thiagom » Ter Nov 02, 2010 18:54
por Thiagom » Ter Nov 02, 2010 18:54
esqueci de dizer, ele pede que nao use lhopital
-
Thiagom
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 02, 2010 17:36
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Moura » Ter Dez 14, 2010 11:55
por Moura » Ter Dez 14, 2010 11:55
P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por MarceloFantini » Ter Dez 14, 2010 13:50
por MarceloFantini » Ter Dez 14, 2010 13:50
Moura, o rapaz pediu para resolver sem L'Hopital como regra do professor.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Moura » Ter Dez 14, 2010 16:40
por Moura » Ter Dez 14, 2010 16:40
Tudo bem, não serve p/ ele, mas pode ser útil p/ outra pessoa.

P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por VtinxD » Sáb Dez 18, 2010 14:34
por VtinxD » Sáb Dez 18, 2010 14:34
Tenho uma ideia espero que esteja certa...não sou um grande conhecedor de limites hehe mas gosto de limites que precisam apenas de manipulações algébricas.
![\lim_{x\rightarrow2}=\frac{\sqrt[3]{5x-2}+\sqrt[3]{8}}{\sqrt[2]{x-1}-1} \lim_{x\rightarrow2}=\frac{\sqrt[3]{5x-2}+\sqrt[3]{8}}{\sqrt[2]{x-1}-1}](/latexrender/pictures/9679ead680d424f566ae214dc39366d0.png)
Agora utilizando a formula dos cubos:

.Sendo
![a=\sqrt[3]{5x-2} a=\sqrt[3]{5x-2}](/latexrender/pictures/ee60c604b6a2c52d9cdfc17dd6adb3bd.png)
e
![b=\sqrt[3]{8} b=\sqrt[3]{8}](/latexrender/pictures/4d4896e7b9ae7153f04f389900a1f4f0.png)
temos:
![\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}=\left(\sqrt[3]{5x-2}-\sqrt[3]{8} \right) \frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}=\left(\sqrt[3]{5x-2}-\sqrt[3]{8} \right)](/latexrender/pictures/9d88f13e227b0f373206658d547cc57e.png)
.Agora jogando no limite,conseguimos:
![\lim_{x\rightarrow2}=\frac{\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}}{\sqrt[2]{x-1}-1} \lim_{x\rightarrow2}=\frac{\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}}{\sqrt[2]{x-1}-1}](/latexrender/pictures/a65827f640f8c3b7e0c02ce5d81fe499.png)
.Arrumando um pouco:
![\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)} \lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}](/latexrender/pictures/6df9f45aa71af00fc73111d0e7d8c350.png)
.Agora multiplicando pelo "conjugado" em baixo e em cima:
![\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}.\frac{\sqrt[2]{x-1}+1}{\sqrt[2]{x-1}+1} \lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}.\frac{\sqrt[2]{x-1}+1}{\sqrt[2]{x-1}+1}](/latexrender/pictures/fdbbd98ec8ba95473be3420d90d9ffc4.png)
![\Rightarrow \lim_{x\rightarrow2}=\frac{5(x-2)(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(x-2)} \Rightarrow \lim_{x\rightarrow2}=\frac{5(x-2)(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(x-2)}](/latexrender/pictures/3d8672ebd6628b4ad5edc58e4d9d4145.png)
.Cortando o (x-2),temos uma função em baixo que só possui raiz complexa e em cima uma que não vai dar zero quando for colocada igual a 2.
![\lim_{x\rightarrow2}=\frac{5(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).}=\frac{5(2)}{(4+4+4)}=\frac{5}{6} \lim_{x\rightarrow2}=\frac{5(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).}=\frac{5(2)}{(4+4+4)}=\frac{5}{6}](/latexrender/pictures/e5a26c3cdebafdb2189873cf10e2370f.png)
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[2]{x-1}-1} \lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[2]{x-1}-1}](/latexrender/pictures/1a995369b61d86c46d174fe2c5af639c.png) tentei multiplicar pelos conjugados, mas da sempre indeterminação, depois tenti multiplicar usando a formula dos cubos, mas mesmo assim anda da indeterminação no numerador... eu não sei mais o que fazer.... a ficha da como resultado: 5/6
tentei multiplicar pelos conjugados, mas da sempre indeterminação, depois tenti multiplicar usando a formula dos cubos, mas mesmo assim anda da indeterminação no numerador... eu não sei mais o que fazer.... a ficha da como resultado: 5/6



![y=\sqrt[n]{u^m}
y=u^\frac{m}{n} y=\sqrt[n]{u^m}
y=u^\frac{m}{n}](/latexrender/pictures/11377ae512e6f68164781bacc89e9c35.png)
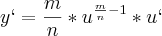
![\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[]{x-1}-1} \lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[]{x-1}-1}](/latexrender/pictures/f2524f9b7bbb771867abdf78bf4cf015.png)

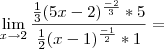
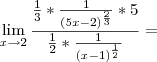
![\lim_{x\rightarrow2}\frac{\frac{5}{3\sqrt[3]{(5x-2)^2}}}{\frac{1}{2 \sqrt[]{x-1}}}= \lim_{x\rightarrow2}\frac{\frac{5}{3\sqrt[3]{(5x-2)^2}}}{\frac{1}{2 \sqrt[]{x-1}}}=](/latexrender/pictures/faad4b3512293be3f18e1bb0d1235e11.png)
![\frac{\frac{5}{3\sqrt[3]{(5*2-2)^2}}}{\frac{1}{2\sqrt[]{2-1}}}= \frac{\frac{5}{3\sqrt[3]{(5*2-2)^2}}}{\frac{1}{2\sqrt[]{2-1}}}=](/latexrender/pictures/3f33784e834f30245fa8c4f116e8e632.png)
![\frac{\frac{5}{3\sqrt[3]{8^2}}}{\frac{1}{2\sqrt[]{1}}}= \frac{\frac{5}{3\sqrt[3]{8^2}}}{\frac{1}{2\sqrt[]{1}}}=](/latexrender/pictures/a4932fa4adc9063a7716a1d6bd8782b5.png)
![\frac{\frac{5}{3\sqrt[3]{64}}}{\frac{1}{2}}= \frac{\frac{5}{3\sqrt[3]{64}}}{\frac{1}{2}}=](/latexrender/pictures/2d7d0c054983784cc915c4aa02a4a60b.png)

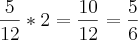




![\lim_{x\rightarrow2}=\frac{\sqrt[3]{5x-2}+\sqrt[3]{8}}{\sqrt[2]{x-1}-1} \lim_{x\rightarrow2}=\frac{\sqrt[3]{5x-2}+\sqrt[3]{8}}{\sqrt[2]{x-1}-1}](/latexrender/pictures/9679ead680d424f566ae214dc39366d0.png)
 .Sendo
.Sendo ![a=\sqrt[3]{5x-2} a=\sqrt[3]{5x-2}](/latexrender/pictures/ee60c604b6a2c52d9cdfc17dd6adb3bd.png) e
e ![b=\sqrt[3]{8} b=\sqrt[3]{8}](/latexrender/pictures/4d4896e7b9ae7153f04f389900a1f4f0.png) temos:
temos:![\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}=\left(\sqrt[3]{5x-2}-\sqrt[3]{8} \right) \frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}=\left(\sqrt[3]{5x-2}-\sqrt[3]{8} \right)](/latexrender/pictures/9d88f13e227b0f373206658d547cc57e.png) .Agora jogando no limite,conseguimos:
.Agora jogando no limite,conseguimos:![\lim_{x\rightarrow2}=\frac{\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}}{\sqrt[2]{x-1}-1} \lim_{x\rightarrow2}=\frac{\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}}{\sqrt[2]{x-1}-1}](/latexrender/pictures/a65827f640f8c3b7e0c02ce5d81fe499.png) .Arrumando um pouco:
.Arrumando um pouco:![\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)} \lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}](/latexrender/pictures/6df9f45aa71af00fc73111d0e7d8c350.png) .Agora multiplicando pelo "conjugado" em baixo e em cima:
.Agora multiplicando pelo "conjugado" em baixo e em cima:![\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}.\frac{\sqrt[2]{x-1}+1}{\sqrt[2]{x-1}+1} \lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}.\frac{\sqrt[2]{x-1}+1}{\sqrt[2]{x-1}+1}](/latexrender/pictures/fdbbd98ec8ba95473be3420d90d9ffc4.png)
![\Rightarrow \lim_{x\rightarrow2}=\frac{5(x-2)(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(x-2)} \Rightarrow \lim_{x\rightarrow2}=\frac{5(x-2)(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(x-2)}](/latexrender/pictures/3d8672ebd6628b4ad5edc58e4d9d4145.png) .Cortando o (x-2),temos uma função em baixo que só possui raiz complexa e em cima uma que não vai dar zero quando for colocada igual a 2.
.Cortando o (x-2),temos uma função em baixo que só possui raiz complexa e em cima uma que não vai dar zero quando for colocada igual a 2.![\lim_{x\rightarrow2}=\frac{5(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).}=\frac{5(2)}{(4+4+4)}=\frac{5}{6} \lim_{x\rightarrow2}=\frac{5(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).}=\frac{5(2)}{(4+4+4)}=\frac{5}{6}](/latexrender/pictures/e5a26c3cdebafdb2189873cf10e2370f.png)
