Complementando a 1ª questão:
Nos dois primeiros
limites, com tendência a +infinito e menos infinito temos uma indeterminação (inf/inf e -inf/-inf).
Podemos utilizar l'Hopital para resolve-la derivando numerador e denominador. Com isso, nos dois casos chegamos ao resultado do
limite igual a 2/3.
O dois outros
limites,
limite lateral pela direita e pela esquerda respectivamente tendendo a 2, podem ser interpretados assim:
Se pegarmos um valor ligeiramente menor que 2, digamos 1.999999999, e substituirmos na função veremos que a tendência é de atingir um valor negativo grande, ou seja, ao nos aproximarmos de 2 pela esquerda a função tenderá a -infinito. De forma semelhante ao nos aproximarmos pela direita a função tenderá a +infinito.
2) Como as alternativas afirmam quanto a inclinação da curva (crescente/decrescente), vamos avaliar o sinal da
derivada primeira. Intervalos de
derivada positiva indicam um intervalo crescente, e negativa intervalos decrescentes.
f '(x) = -12/(3x-6)²
O denominador (3x-6)² é sempre positivo, logo a
derivada será sempre negativa e, portanto, a curva é decrescente em todo seu domínio. Veja parte dessa curva:

- Sem título.png (9.1 KiB) Exibido 61956 vezes
3) As alternativas aqui abordam a concavidade da curva. Como a
derivada segunda f ''(x) = 8/[3(x-2)³] não possui zeros (verificar!), ou seja, possíveis inflexões da curva, vamos dividir a analise na sua indeterminação (x=2).
A concavidade é dada pelo sinal da
derivada segunda, se positiva a concavidade é para cima, se negativa concavidade para baixo.
Para x<2 a
derivada segunda tem valores negativos, logo concavidade para baixo.
Para x>2 a
derivada segunda tem valores positivos, logo concavidade para cima.
I -> Errada
II -> Certo
III -> Certo
Qualquer duvida, deixa msg.

























 Super mega obrigado!!!!!!
Super mega obrigado!!!!!!





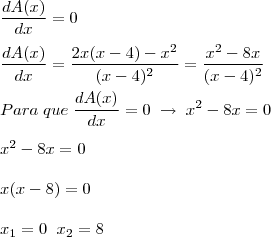






























 muito muito obrigada!!
muito muito obrigada!!













 , acima do eixo das abscissas, e entre as retas verticais x=1 e x=3.
, acima do eixo das abscissas, e entre as retas verticais x=1 e x=3.

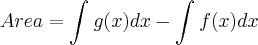
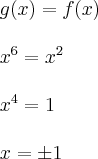
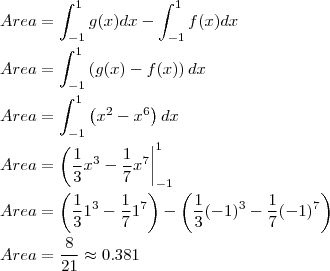









 .
.
 :
: