 por Camila Albiero Iuspa » Ter Ago 14, 2012 21:42
por Camila Albiero Iuspa » Ter Ago 14, 2012 21:42
Olá, como vai?
Gostaria de tirar uma dúvida deste problema também:
Pablo propôs o seguinte desafio: "Para jogar futebol na praia, eu e meu irmão construímos uma trave de gol com medidas bem menores que a oficial. Cada uma das traves media exatamente metade da minha altura. Num dia de muito sol, medimos a sombra de uma das traves e obtivemos 45 cm a mais do que a medida da própria trave. Nesse mesmo instante, somando a minha altura com a sombra que eu projetava, encontramos 4,5 m. Quanto eu tenho de altura? "
Aguardo resposta.
-
Camila Albiero Iuspa
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Ago 12, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: pedagogia
- Andamento: formado
 por e8group » Ter Ago 14, 2012 21:53
por e8group » Ter Ago 14, 2012 21:53
Camila Albiero Iuspa ,boa noite .
Quanto a sua dúvida ,perceba que :
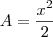
,donde x é o cateto do triângulo isósceles .
Precisamos achar o valor para x tal que a hipotenusa seja igual a 12 m,para isso aplique T. Pitágoras .(

)
Neste caso ,
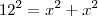
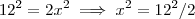
.Assim ,
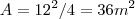
OBS.: Sempre post em um novo tópico .
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria
por ehrefundini » Ter Abr 22, 2008 16:53
- 3 Respostas
- 7326 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:57
Pedidos de Materiais
-
- geometria 2
por ehrefundini » Qua Mai 07, 2008 10:35
- 1 Respostas
- 6041 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 10:59
Pedidos de Materiais
-
- Geometria
por rybb » Ter Ago 25, 2009 07:48
- 1 Respostas
- 2872 Exibições
- Última mensagem por Elcioschin

Seg Out 05, 2009 22:41
Trigonometria
-
- Geometria - help me?
por rybb » Ter Ago 25, 2009 07:55
- 3 Respostas
- 7317 Exibições
- Última mensagem por Molina

Qua Ago 26, 2009 23:18
Geometria
-
- geometria
por cristina » Qui Nov 19, 2009 07:05
- 0 Respostas
- 2468 Exibições
- Última mensagem por cristina

Qui Nov 19, 2009 07:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


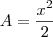 ,donde x é o cateto do triângulo isósceles .
,donde x é o cateto do triângulo isósceles . )
)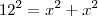
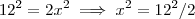 .Assim ,
.Assim ,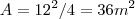

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.