 por luizmario » Ter Jul 10, 2012 13:16
por luizmario » Ter Jul 10, 2012 13:16
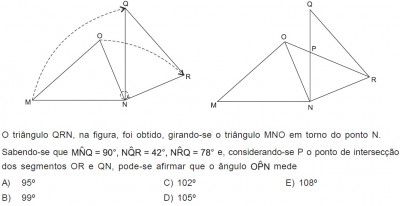
O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que MNM=90°,NQR=42°,NRQ=78° e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo OPN mede.
A resposta correta é 105°,porém sempre outro que resultado
Prezado
luizmario,
Por favor, antes de postar um tópico leia as regras deste fórum:
viewtopic.php?f=9&t=7543Em especial, vide a regra 3.
Por favor, corrija esse problema.
Atenciosamente,
Equipe de Moderadores.[/quote]
- Anexos
-
-
luizmario
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jul 09, 2012 09:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Jul 10, 2012 14:53
por LuizAquino » Ter Jul 10, 2012 14:53
luizmario escreveu: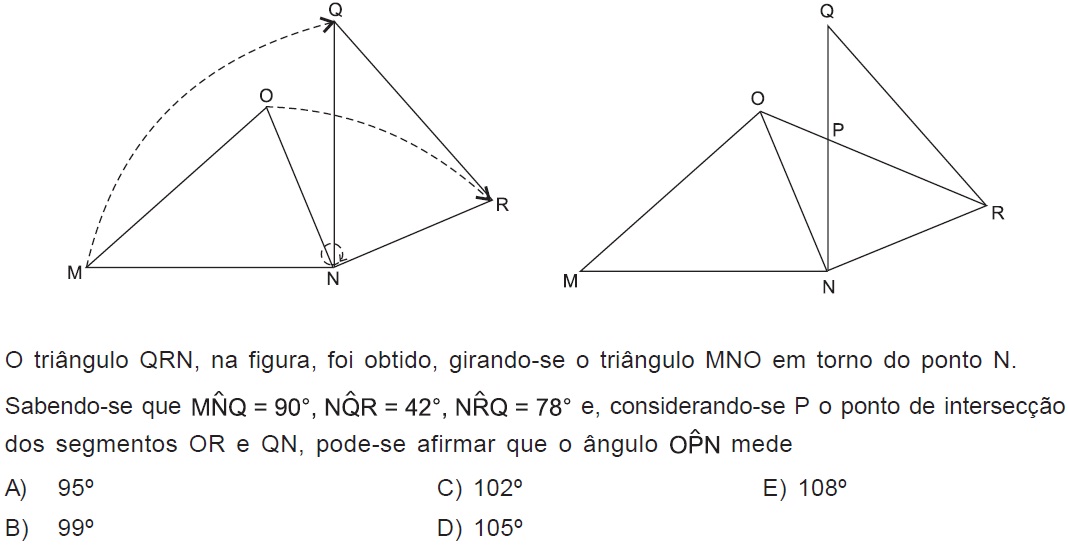
O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que MNM=90°,NQR=42°,NRQ=78° e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo OPN mede.
A resposta correta é 105°,porém sempre outro que resultado
Observe a figura abaixo. Os ângulos em verde foram dados no problema. Os ângulos em vermelho podemos calcular.
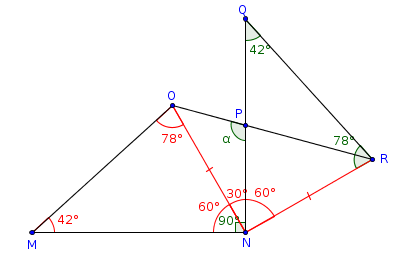
- figura1.png (15.62 KiB) Exibido 2566 vezes
Do triângulo QRN, foram dados os ângulos

e
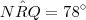
. Portanto, temos que
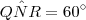
.
Os triângulos MNO e QRN são congruentes, já que um é apenas uma rotação do outro. Sendo assim, os seus ângulos internos correspondentes possuem as mesmas medidas. Teremos que
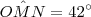
,
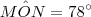
e

.
Como
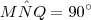
e
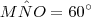
, temos que
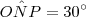
. Disso concluímos que

.
Novamente, como os triângulos MNO e QRN são congruentes, os seus lados correspondentes possuem as mesmas medidas. Temos então que

. Sendo assim, o triângulo ONR é isósceles, sendo que o ângulo oposto a base mede 90º.
Agora tente finalizar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UEFS) Conjuntos
por 13run0 » Sex Mai 28, 2010 15:54
- 3 Respostas
- 1748 Exibições
- Última mensagem por Molina

Dom Mai 30, 2010 15:23
Álgebra Elementar
-
- cefet-mg 2012
por Thulio_Parazi » Ter Abr 10, 2012 09:55
- 1 Respostas
- 1597 Exibições
- Última mensagem por MarceloFantini

Ter Abr 10, 2012 21:12
Trigonometria
-
- cefet-mg 2012 log
por Thulio_Parazi » Ter Abr 10, 2012 14:37
- 5 Respostas
- 3749 Exibições
- Última mensagem por Thulio_Parazi

Qui Abr 12, 2012 09:26
Logaritmos
-
- Questão CEFET-MG 2012
por Thulio_Parazi » Qui Abr 05, 2012 13:48
- 5 Respostas
- 4819 Exibições
- Última mensagem por fraol

Ter Abr 10, 2012 20:02
Trigonometria
-
- Cefet-mg 2012 questão 03
por Thulio_Parazi » Sex Abr 13, 2012 11:12
- 4 Respostas
- 4488 Exibições
- Última mensagem por fraol

Qua Abr 18, 2012 22:26
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e 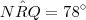 . Portanto, temos que
. Portanto, temos que 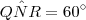 .
.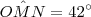 ,
, 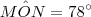 e
e  .
.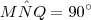 e
e 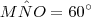 , temos que
, temos que 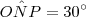 . Disso concluímos que
. Disso concluímos que  .
. . Sendo assim, o triângulo ONR é isósceles, sendo que o ângulo oposto a base mede 90º.
. Sendo assim, o triângulo ONR é isósceles, sendo que o ângulo oposto a base mede 90º.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.