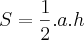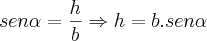por matII » Seg Abr 30, 2012 09:12
por matII » Seg Abr 30, 2012 09:12
Galera, tentei fazer essa questão de alguns jeitos, mas nunca conseguia terminar. Preciso de ajuda.
Questão...
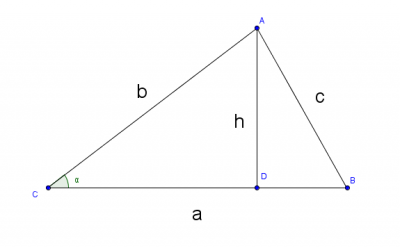
Mostre que a área de um triângulo ABC é S=1/2bc . sen Â
Obs: O bc . sen  multiplica o 1 e não o 2.
Agradeço a quem ajudar.
Abraços.
-
matII
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Abr 30, 2012 08:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Edu-sjc » Seg Abr 30, 2012 14:11
por Edu-sjc » Seg Abr 30, 2012 14:11
Sabemos que a área do triângulo ABC é dado por:
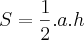
Agora, no triângulo ADC observamos que:
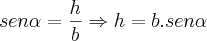
Substituindo h teremos:

- Anexos
-
-
Edu-sjc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Out 26, 2011 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão geometria plana relacionada aos ângulos notáveis]
 por Anniemf » Qua Mar 28, 2012 14:33
por Anniemf » Qua Mar 28, 2012 14:33
- 1 Respostas
- 3551 Exibições
- Última mensagem por kelvinJhonson

Sáb Abr 21, 2012 23:20
Geometria Plana
-
- Taxa relacionada
por Viviani » Ter Mar 05, 2013 23:00
- 1 Respostas
- 1349 Exibições
- Última mensagem por Russman

Qua Mar 06, 2013 02:40
Cálculo: Limites, Derivadas e Integrais
-
- Situação e Equação Relacionada
por ShadowOnLine » Sáb Jul 19, 2014 14:39
- 1 Respostas
- 1062 Exibições
- Última mensagem por Russman

Sáb Jul 19, 2014 15:33
Equações
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8718 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4698 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.