 por Pri Ferreira » Qui Mar 15, 2012 18:03
por Pri Ferreira » Qui Mar 15, 2012 18:03
Professora Tháis comprou um sítio do Pica Pau Amarelo, mas se deparou com uma questão: 20% do total da sua propriedade corresponde a uma reserva ambiental. Thaís sabe que o sítio tem duas fases: uma semicircular, cujo raio mede 80 e uma retangular, cujo lado maior mede 200 m (considere pi=3), logo a área correspondente à reserva ambiental é, em m²:
a) 35200
b) 7040
c) 19200
d) 16000
e) 3200
Já tentei encontrei outro valor q naum está entre as opções. Encontrei 8320!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por emsbp » Qui Mar 15, 2012 18:36
por emsbp » Qui Mar 15, 2012 18:36
Boa noite.
De facto, resolvendo segundo os dados do problema também chego ao mesmo valor:8320
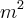
.
Segui o seguinte raciocínio:
Área total= área do semicírculo + área do retângulo.
Área semicírculo =3*80*80/2=19200/2=
Área do rectângulo= 200*(80+80)=32000
Área total= 9600+32000=41600
Reserva=0.2*41600=8320
Ou o enunciado não está bem formulado ou então as hipóteses não estão corretas.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2899 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- area de um retangulo
por lais1906 » Sáb Out 13, 2012 12:32
- 3 Respostas
- 3052 Exibições
- Última mensagem por e8group

Sáb Out 20, 2012 10:17
Trigonometria
-
- [Otimização]Maior área de um retângulo
por frank1 » Qua Mai 23, 2012 03:29
- 8 Respostas
- 17543 Exibições
- Última mensagem por adauto martins

Qui Jun 06, 2019 12:59
Cálculo: Limites, Derivadas e Integrais
-
- [Área de Triângulo Retângulo] Teorema de Pitágoras
 por RMedeirosCosta » Qua Abr 29, 2015 23:21
por RMedeirosCosta » Qua Abr 29, 2015 23:21
- 0 Respostas
- 2277 Exibições
- Última mensagem por RMedeirosCosta

Qua Abr 29, 2015 23:21
Trigonometria
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4035 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.