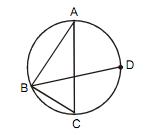
Eduardo Goncalves escreveu:Na figura, AB = 4, BC = 2, AC é diâmetro e os ângulos ABD e CBD são iguais. A medida da corda BD é:
- figura_da_questão.jpg (3.42 KiB) Exibido 7329 vezes
Sabemos que o ângulo ABC é 90º.
Consegui achar por Pitágoras o valor de AC.
Considerando P o ponto de intersecção de AC e BD.
Pelos dados, BP é bissetriz de 90º.
Pelo teorema da bissetriz, temos que AP/4 = CP/2. Então AP = 2CP.
Mas não consegui encontrar outra relação para achar BD.
Considere a figura abaixo.
- figura.png (7.79 KiB) Exibido 7329 vezes
O ponto O é o centro da circunferência. O arco CD mede 90º, pois o seu ângulo inscritos correspondente mede 45º. Dessa forma, o ângulo central COD mede 90º.
Chamando de x a medida de CP, você já sabe que AP = 2x. Note que com isso, temos que AC = 3x. Aplicando o Teorema de Pitágoras no triângulo retângulo ABC, podemos determinar a medida de AC e consequentemente o valor de x.
Considerando o triângulo retângulo DOP, o cateto OD corresponde ao raio da circunferência (e portanto OD = AC/2). Já o cateto OP é igual a OC - x (sendo que OC é outro raio da circunferência). Considerando que as medidas dos catetos OD e OP já serão conhecidas, podemos calcular o valor da hipotenusa PD.
Considerando agora o triângulo PBC, já conhecemos as medidas de seus lados BC e CP. Aplicando a
Lei dos Cossenos, podemos obter a medida de seu lado BP.
Como já conhecemos as medidas de BP e PD, podemos calcular a medida de BD, já que BD = BP + PD.
Agora basta você terminar o exercício.
