 por lukasmetal » Qua Nov 30, 2011 12:11
por lukasmetal » Qua Nov 30, 2011 12:11
Sou novo no frum, Tirei um print de uma questão em pdf. Me desculpem por qualquer incoviniente.
Não estou conseguindo resolver essa questão, não sei qual fórmula empregar.
Como eu iria saber os lados triãngulo através da área? Ou eu estou fazendo a pergunta errada?
- Anexos
-
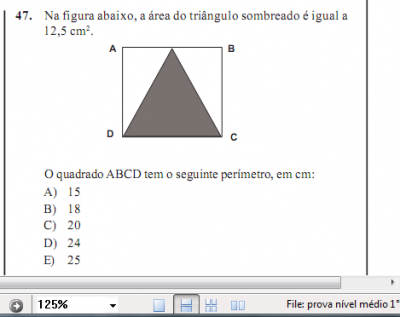
- Questão 47
-
lukasmetal
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 30, 2011 01:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por albertns » Qua Nov 30, 2011 22:18
por albertns » Qua Nov 30, 2011 22:18
Seja L o lado do quadrado, assim o perimetro do quadrado é 4L.
A altura do triangulo é h e é igual a L.
Assim temos que a área do triangulo é A = B.H/2, ou seja, é a base L x altura L / 2.
então temos que a área do triangulo é A = LxL/2
12,5 x 2 = LxL
L = 5.
O perimetro é então 4 x 5 = 20.
Resposta C;
-
albertns
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 30, 2011 12:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: computação
- Andamento: formado
 por MarceloFantini » Qui Dez 01, 2011 01:40
por MarceloFantini » Qui Dez 01, 2011 01:40
Você tem que saber a expressão da área do triângulo, que depende dos seus lados. Note que neste caso a base e altura mais naturais são iguais, chamando L do lado do quadrado (e coincidentemente do triângulo), temos

, daí

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lukasmetal » Qui Dez 01, 2011 12:19
por lukasmetal » Qui Dez 01, 2011 12:19
Nossa, muito obrigado aos dois, me ajudaram bastante. Vou estudar mais geomtria plana. Abraços =)
-
lukasmetal
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 30, 2011 01:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Triangulo e quadrado, perimetro constante
 por heldersmd » Sáb Set 15, 2012 12:42
por heldersmd » Sáb Set 15, 2012 12:42
- 1 Respostas
- 1497 Exibições
- Última mensagem por young_jedi

Sáb Set 15, 2012 14:54
Geometria Plana
-
- Calcular Área no Gráfico através de uma Função
por joedsonazevedo » Qui Nov 15, 2012 11:11
- 1 Respostas
- 1723 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 14:07
Funções
-
- Como calcular a área do triângulo inscrito
 por Guga1981 » Ter Mai 29, 2018 17:39
por Guga1981 » Ter Mai 29, 2018 17:39
- 3 Respostas
- 7514 Exibições
- Última mensagem por Guga1981

Sex Jun 01, 2018 21:35
Geometria Plana
-
- Calcular primitiva atraves do metodo se substituiçao
por rodrigonapoleao » Seg Dez 17, 2012 17:25
- 1 Respostas
- 1607 Exibições
- Última mensagem por e8group

Qua Dez 26, 2012 21:22
Cálculo: Limites, Derivadas e Integrais
-
- Perímetro do triângulo
por maria cleide » Sáb Mai 28, 2011 16:49
- 3 Respostas
- 3907 Exibições
- Última mensagem por MarceloFantini

Dom Mai 29, 2011 19:55
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , daí
, daí  .
.






