 por Mi_chelle » Seg Abr 25, 2011 15:21
por Mi_chelle » Seg Abr 25, 2011 15:21
Não consigo resolver esse problema:
As bicicletas possuem uma corrente que liga uma coroa dentada dianteira, movimentada pelos pedais, a uma coroa localizada no eixo da roda traseira.
O número de voltas dadas pela roda traseira, a cada pedalada, depende do tamanho relativo dessas coroas.
a) Suponhando que o diâmetro da coroa dianteira seja D2=30cm, o da coroa traseira, D1=10cm, e o diâmetro da roda traseira seja Dr= 80cm, calcule o deslocamento aproximado efetuado pela bicicleta quando o ciclista dá uma pedalada (considere pi=3).
b)Caso a bicicleta possua marchas , cada marcha é uma combinação de uma das coroas traseiras, qual é o possivel total de marchas, tendo em vista que ela possui duas coroas dianteiras e cinco traseiras?
Resposta Gabarito: a)2,4m e b)10 marchas.
A questão b, imaginando que cada marcha seria a combinação de uma das coroas traseira, com uma da dianteira fiz:
2x15=10 marchas.
Poirém a questão a, não consigo desenvolver, comecei calculando o deslocamento da coroa dianteira:
Variação angular= Deslocamento/ Raio
Deslocamento= 3x15
Deslocamento= 45
Não sei se iniciei corretamente e não consigo imaginar o que fazer depois disso.
-
Mi_chelle
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Mar 28, 2011 17:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Química
- Andamento: formado
 por FilipeCaceres » Seg Abr 25, 2011 20:25
por FilipeCaceres » Seg Abr 25, 2011 20:25
a)Observe que ao darmos uma peladada completa a coroa traseira dará 3 voltas,pois a coroa dianteira de 3 vezes maior.
Como a coroa traseira esta ligada diretamente na roda esta por sua vez também dará 3 voltas, sendo assim temos,
Deslocamento:
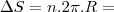
, n é o número de voltas e R o raio da roda.
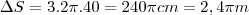
Como o enúnciado diz para utilizarmos

temos,
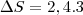
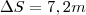
b) Como cada coroa dianteira pode fazer combinação com 5 coroa traseira, temos
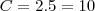
possibilidades.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Mi_chelle » Qui Abr 28, 2011 01:47
por Mi_chelle » Qui Abr 28, 2011 01:47
Muito obrigada pela ajuda!!
-
Mi_chelle
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Mar 28, 2011 17:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Química
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida]Um desafio que envolve probabilidade
por Gabi Biel » Qui Out 17, 2013 20:37
- 5 Respostas
- 3826 Exibições
- Última mensagem por temujin

Sáb Out 19, 2013 21:05
Probabilidade
-
- Dúvida de Física - Lei de Coulomb.
por Sobreira » Dom Mai 05, 2013 16:41
- 4 Respostas
- 1745 Exibições
- Última mensagem por Russman

Dom Mai 05, 2013 20:57
Álgebra Elementar
-
- Dúvida Física - Dipolo elétrico.
 por Sobreira » Ter Mai 21, 2013 02:01
por Sobreira » Ter Mai 21, 2013 02:01
- 0 Respostas
- 696 Exibições
- Última mensagem por Sobreira

Ter Mai 21, 2013 02:01
Aritmética
-
- Calculo que envolve PA e PG
por andersontricordiano » Qua Mar 16, 2011 12:21
- 1 Respostas
- 2214 Exibições
- Última mensagem por Molina

Qua Mar 16, 2011 14:05
Progressões
-
- Calculo que envolve PG
por andersontricordiano » Qui Mar 31, 2011 02:19
- 3 Respostas
- 1757 Exibições
- Última mensagem por FilipeCaceres

Qui Mar 31, 2011 17:35
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


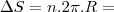 , n é o número de voltas e R o raio da roda.
, n é o número de voltas e R o raio da roda.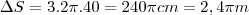
 temos,
temos,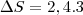
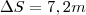
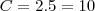 possibilidades.
possibilidades.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.