 por Balanar » Seg Ago 30, 2010 20:24
por Balanar » Seg Ago 30, 2010 20:24
Por um ponto P de uma reta r traçam-se do mesmo lado de r, duas semi-retas. Calcular os três ângulos formados sabendo-se que suas medidas, expressas em graus, são números consecutivos.
Resposta:
59,60 e 61 graus.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Ago 30, 2010 23:28
por Molina » Seg Ago 30, 2010 23:28
Balanar escreveu:Por um ponto P de uma reta r traçam-se do mesmo lado de r, duas semi-retas. Calcular os três ângulos formados sabendo-se que suas medidas, expressas em graus, são números consecutivos.
Resposta:
59,60 e 61 graus.
Boa noite.
Como essa reta e as duas semi-retas formarão um triângulo e sabemos que a soma dos três ângulos internos de um triângulo é 180°, temos que:
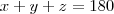
onde x, y e z são os ângulos internos do triângulo.
Supondo, sem perda de generalidade, que

.
Como eles são consecutivos podemos escrever:
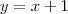
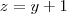
E substituindo na primeira equação:
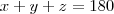
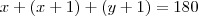
![x + (x+1) + [(x+1)+1] = 180 x + (x+1) + [(x+1)+1] = 180](/latexrender/pictures/449c7f4efcf90b22709c8966644eab03.png)
Você chegou em uma equação com uma variável apenas.
Agora é fácil descobrir x e posteriormente os outros ângulos.
Qualquer dúvida, informe.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ângulo/circunferência] Ângulo CÂB, ajude-me!
 por miltonsermoud » Qua Set 30, 2015 17:14
por miltonsermoud » Qua Set 30, 2015 17:14
- 3 Respostas
- 3503 Exibições
- Última mensagem por miltonsermoud

Sex Out 02, 2015 07:41
Geometria Plana
-
- angulo
por cristina » Qua Set 23, 2009 00:08
- 4 Respostas
- 2795 Exibições
- Última mensagem por cristina

Ter Set 29, 2009 11:28
Trigonometria
-
- Angulo
por Thays » Ter Jan 17, 2012 14:21
- 1 Respostas
- 1691 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 17, 2012 14:37
Sistemas de Equações
-
- Angulo
por Thays » Sex Jan 27, 2012 10:49
- 1 Respostas
- 1769 Exibições
- Última mensagem por Molina

Sex Jan 27, 2012 13:47
Sistemas de Equações
-
- Ângulo
por ulisses123 » Seg Jul 14, 2014 13:36
- 0 Respostas
- 980 Exibições
- Última mensagem por ulisses123

Seg Jul 14, 2014 13:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



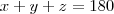
 .
.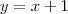
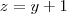
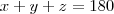
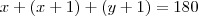
![x + (x+1) + [(x+1)+1] = 180 x + (x+1) + [(x+1)+1] = 180](/latexrender/pictures/449c7f4efcf90b22709c8966644eab03.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
