(escola militar do realengo-exame de admissao 1936)
divide-se o lado BC de um trapezio em dois segmentos BF e CF,proporcionais a 3 e 2 e,pelo ponto de divisao f,
traça-se uma reta EF paralela as bases.calcular EF sabendo que AB=38,5m e DC=12,45m.



 ,a qual nao precisaremos de usar aqui e sim o "teorema de tales,das paralelas" e semelhança de triangulos.vamos a soluçao:
,a qual nao precisaremos de usar aqui e sim o "teorema de tales,das paralelas" e semelhança de triangulos.vamos a soluçao: .bom agora temos parte do segmento EF,pedido pelo problema.
.bom agora temos parte do segmento EF,pedido pelo problema.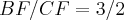 .bom usaremos agora semelhança dos triangulos BCD e BFP,onde p,é ponto de encontro da diagonal BD,com o segmento EF,ponto esse que é tambem limitante da "mediana de euler",que calculamos.logo,teremos:
.bom usaremos agora semelhança dos triangulos BCD e BFP,onde p,é ponto de encontro da diagonal BD,com o segmento EF,ponto esse que é tambem limitante da "mediana de euler",que calculamos.logo,teremos: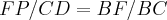 ,que calculamos das semelhanças dos ditos triangulos,logo:
,que calculamos das semelhanças dos ditos triangulos,logo: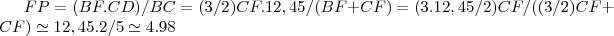
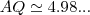
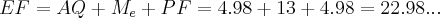

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)