A progressão geométrica consiste em encontrarmos o lado 'x' fo triângulo equilátero, seu perímetro 3x e a área do mesmo.
Vamos calcular a altura deste triângulo de três lados iguais, de base b = x e hipotenusa x. Usando Pitágoras, tem-se que:

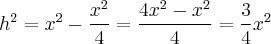
![h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2} h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2}](/latexrender/pictures/fe40ecaac1b798d4c5baa0bea0fb5f56.png)
A área deste triângulo será;
![A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4} A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4}](/latexrender/pictures/4e47c625296e653b92f2f10a9358925d.png)
Então, nossa sequência será:
![\left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right ) \left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right )](/latexrender/pictures/f7198fa8e453700ff7a859cad6cf1ef6.png)
A razão desta PG é obtida dividindo-se o valor subsequente pelo seu antecessor, assim:
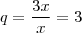
![q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12} q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12}](/latexrender/pictures/19df440a9936fcd0910d1cfb8cadf6c1.png)
7
Dos dois resultados acima, sabemos que as duas razões obtidas deverão ser iguais. Assim,
![\frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}} \frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}}](/latexrender/pictures/357097312c887481a05999c6ddbee626.png)
Racionalizando, ou seja, multiplicando-se o numerador e o denominador por raiz de três, teremos:
![x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3} x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3}](/latexrender/pictures/918f8a846b4fb6becd4b060da790c9b0.png)
Por fim, nossa PG terá a seguinte sequência:
![\left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right) \left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right)](/latexrender/pictures/748cee0e8a67f449bf23beb55b639787.png)
E portanto, a resposta é a letra (a)!

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



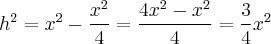
![h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2} h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2}](/latexrender/pictures/fe40ecaac1b798d4c5baa0bea0fb5f56.png)
![A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4} A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4}](/latexrender/pictures/4e47c625296e653b92f2f10a9358925d.png)
![\left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right ) \left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right )](/latexrender/pictures/f7198fa8e453700ff7a859cad6cf1ef6.png)
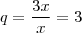
![q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12} q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12}](/latexrender/pictures/19df440a9936fcd0910d1cfb8cadf6c1.png) 7
7![\frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}} \frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}}](/latexrender/pictures/357097312c887481a05999c6ddbee626.png)
![x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3} x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3}](/latexrender/pictures/918f8a846b4fb6becd4b060da790c9b0.png)
![\left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right) \left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right)](/latexrender/pictures/748cee0e8a67f449bf23beb55b639787.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)