 por Padoan » Qui Fev 11, 2010 18:36
por Padoan » Qui Fev 11, 2010 18:36
E aqui... eu também estava em dúvida nessa:
Em um triângulo equilátero, ABE, cujo lado mede a , e um quadrado, BCDE, cujo lado também mede a. Com base nessas informações, é CORRETO afirmar que a área do triângulo
ABC é
a) a² / 3
b) a² / 4
c) a² ?3 / 4
d) a² ?3 / 4
No caso seria uma piramide quadrangular com os lados de valor a, então eu fiz da seguinte forma:
a = l² ?3 /4
a = a² ?3/4
Beleza, opção C, porém no gabarito diz ser opção B... alguem saberia me ajudar?
-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sex Fev 12, 2010 01:10
por MarceloFantini » Sex Fev 12, 2010 01:10
Boa noite Padoan.
O triângulo pedido não é equilátero. Veja o desenho:

Para calcular a área basta usar:
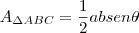
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Padoan » Sex Fev 12, 2010 12:13
por Padoan » Sex Fev 12, 2010 12:13
Ainda estou meio boiando...
Tipo, temos um quadrado de valores = a, um triangulo equilatero de lados de valores = a e temos que descobrir a area de um triangulo com base = a e um lado = a... ainda não entendi S:
Edit:
Aqui, consegui passar a imagem para cá... acabou que eu pensei que era uma piramide, eu so retardado auhauhau

-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sex Fev 12, 2010 13:03
por Molina » Sex Fev 12, 2010 13:03
Temos que trata-se de um triângulo isósceles com dois lados
a e o lado AC (base do triângulo) que não conhecemos. Temos a informação que o ângulo B vale
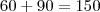
graus. E com isso sabemos os dois outros ângulos, já que é um triângulo isósceles: os ângulos A e C possuem 15 graus.
Acho que podemos encontrar o valor do segmento AC usando a lei dos seno ou a lei do cosseno.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Padoan » Sex Fev 12, 2010 13:08
por Padoan » Sex Fev 12, 2010 13:08
Ah, eu pedi pro professor de física... matemática só semana que vem D:
Ele disse isso mesmo, tinha que usar lei do seno/cosseno
Tenso que isso eu ainda não aprendi no colégio.
Mas como voce soube que B vale 150?
-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sex Fev 12, 2010 13:11
por Molina » Sex Fev 12, 2010 13:11
Padoan escreveu:Mas como voce soube que B vale 150?
O ângulo do triângulo é 60 graus, pois trata-se de um triângulo equilátero. E o ângulo do quadrado é 90 graus. Somando os dois chegamos em 150 graus.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Sex Fev 12, 2010 13:42
por MarceloFantini » Sex Fev 12, 2010 13:42
Boa tarde.
Não é para calcular o outro lado, portanto não precisa usar teorema do seno ou cosseno. Basta usar o teorema de calcular a área tendo dois lados e o ângulo entre eles (não sei se tem nome ao certo). Veja:
 Demonstração
DemonstraçãoSeja o triângulo

um triângulo qualquer e

sua altura. Sua área é definida como:
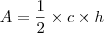
Calculando o seno de alpha, vemos que:
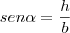
Portanto:
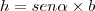
Logo, encontramos que a área de um triângulo qualquer pode ser calculada como:
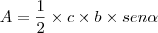
Esse teorema é importante e prático, procure lembrar dele.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4408 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2992 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Área do Triângulo
por Cleyson007 » Sex Mai 14, 2010 13:07
- 1 Respostas
- 2321 Exibições
- Última mensagem por Douglasm

Sex Mai 14, 2010 13:38
Geometria Analítica
-
- Área do Triângulo
por valeuleo » Ter Abr 05, 2011 11:25
- 1 Respostas
- 2686 Exibições
- Última mensagem por LuizAquino

Ter Abr 05, 2011 11:42
Geometria Analítica
-
- Área de triângulo
por Mi_chelle » Qua Mai 04, 2011 20:16
- 2 Respostas
- 6063 Exibições
- Última mensagem por FilipeCaceres

Ter Jun 14, 2011 23:41
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



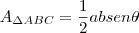



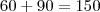 graus. E com isso sabemos os dois outros ângulos, já que é um triângulo isósceles: os ângulos A e C possuem 15 graus.
graus. E com isso sabemos os dois outros ângulos, já que é um triângulo isósceles: os ângulos A e C possuem 15 graus.

 um triângulo qualquer e
um triângulo qualquer e  sua altura. Sua área é definida como:
sua altura. Sua área é definida como: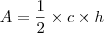
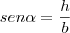
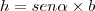
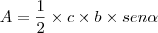
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.