![ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}} ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}}](/latexrender/pictures/eaaaed059e85ac13ac01bba6161caa5b.png) ( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²
( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²COM essa fórmula eu tentei calcular o seno de 22,5 (22,5 mesmo e não 22,5º)
e encontrei
![\frac{\sqrt[]{2-\sqrt[]{2}}}{2} \frac{\sqrt[]{2-\sqrt[]{2}}}{2}](/latexrender/pictures/3f3ec9ad373da76348e7f8f1c4531da8.png) ( está correto?)
( está correto?)porem não consegui calcular o cosseno.
Ajude-me por favor

![ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}} ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}}](/latexrender/pictures/eaaaed059e85ac13ac01bba6161caa5b.png) ( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²
( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²![\frac{\sqrt[]{2-\sqrt[]{2}}}{2} \frac{\sqrt[]{2-\sqrt[]{2}}}{2}](/latexrender/pictures/3f3ec9ad373da76348e7f8f1c4531da8.png) ( está correto?)
( está correto?)
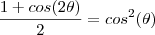
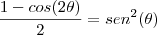
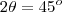




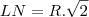
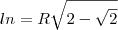
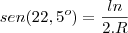
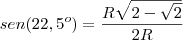
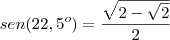
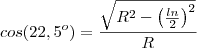
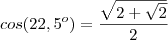


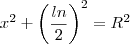
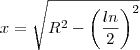
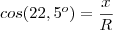
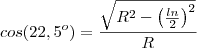

![\frac{\sqrt[]{{\frac{R\sqrt[]{2-\sqrt[]{2}}}{2}}^{2}} - {R}^{2} }{R} \frac{\sqrt[]{{\frac{R\sqrt[]{2-\sqrt[]{2}}}{2}}^{2}} - {R}^{2} }{R}](/latexrender/pictures/24a9482c4cc80b760b77271f8fcdd635.png)

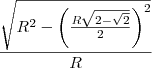
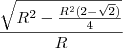
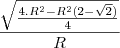
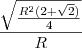
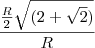
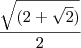


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante