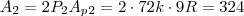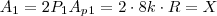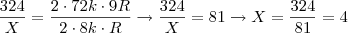por atpe » Qui Set 16, 2010 20:13
por atpe » Qui Set 16, 2010 20:13
Quem me ajuda com este?
A área de 1 octógono regular é de 324m^2. Determine a área de 1 outro octogono regular cujo perimetro é a nona parte do octógono anterior.
O resultado nas soluçoes dá 4m^2.
A unica formula que vem no meu livro é Area=2.Perimetro.apotema. Desta forma não estou conseguindo. Ja pesquisei e apenas aparecem formulas mais avançadas.
Obrigada
-
atpe
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Set 16, 2010 20:08
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: naotenho
- Andamento: cursando
 por MarceloFantini » Sex Set 17, 2010 00:21
por MarceloFantini » Sex Set 17, 2010 00:21
O perímetro e o raio da circunferência inscrita são diretamente proporcionais. Portanto, se o lado do menor é

, o perímetro é

, e o perímetro do maior é
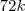
. Portanto, se o perímetro aumentou nove vezes, o raio inscrito também aumentou nove vezes, de modo que

. Portanto:
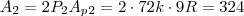
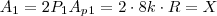
Dividindo:
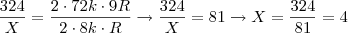
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- área do octógono
 por maria cleide » Qui Mai 12, 2011 17:43
por maria cleide » Qui Mai 12, 2011 17:43
- 12 Respostas
- 17997 Exibições
- Última mensagem por claudinho

Ter Jun 14, 2011 03:56
Geometria Plana
-
- Área dentro de um octógono
por anfran1 » Dom Ago 19, 2012 12:06
- 3 Respostas
- 2601 Exibições
- Última mensagem por anfran1

Dom Nov 17, 2013 10:34
Geometria Plana
-
- [ área do octógono] ajudem por favor...
por jeanderson09 » Qui Out 11, 2012 21:23
- 2 Respostas
- 1849 Exibições
- Última mensagem por jeanderson09

Qui Out 11, 2012 22:10
Geometria Plana
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6560 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11346 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , o perímetro é
, o perímetro é  , e o perímetro do maior é
, e o perímetro do maior é 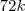 . Portanto, se o perímetro aumentou nove vezes, o raio inscrito também aumentou nove vezes, de modo que
. Portanto, se o perímetro aumentou nove vezes, o raio inscrito também aumentou nove vezes, de modo que  . Portanto:
. Portanto: