 por Marcelo C Delgado » Sex Set 10, 2010 18:29
por Marcelo C Delgado » Sex Set 10, 2010 18:29
Pessoal, estou precisando de uma ajuda de como resolver o exercício abaixo, cito:
Um recipiente utilizado para armazenagem que tem seu formato cônico de base circular reta, possui uma altura que mede 30cm. Ao retirar o tronco desse cone percebemos que a base menor "r" está paralela a base maior "R" e possui um diametro de 6cm, sendo que a altura do cone retirado é de 5cm. Qual o volume desse tronco?
Fico no aguardo de uma solução.
Att.
Marcelo
-
Marcelo C Delgado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Set 10, 2010 18:08
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico Mecânico
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Volume do tronco da pirâmide
 por erikamurizinepires12 » Qui Fev 09, 2017 16:02
por erikamurizinepires12 » Qui Fev 09, 2017 16:02
- 1 Respostas
- 8262 Exibições
- Última mensagem por 314159265

Seg Fev 13, 2017 02:31
Geometria Espacial
-
- [Geometria Espacial] Volume do tronco do cone
por jukkax » Sáb Out 19, 2013 21:32
- 1 Respostas
- 3564 Exibições
- Última mensagem por young_jedi

Dom Out 20, 2013 22:43
Geometria Espacial
-
- [Dúvida]Aplicações de Integração - Volume do Tronco de Cone
 por Jhonata » Dom Jun 10, 2012 12:45
por Jhonata » Dom Jun 10, 2012 12:45
- 2 Respostas
- 9428 Exibições
- Última mensagem por Jhonata

Ter Jun 12, 2012 12:20
Cálculo: Limites, Derivadas e Integrais
-
- Tronco de cone
 por Ananda » Ter Abr 01, 2008 19:38
por Ananda » Ter Abr 01, 2008 19:38
- 5 Respostas
- 13246 Exibições
- Última mensagem por Ananda

Qua Abr 02, 2008 13:48
Geometria Espacial
-
- tronco de pirâmide
por von grap » Ter Jun 19, 2012 12:04
- 0 Respostas
- 1881 Exibições
- Última mensagem por von grap

Ter Jun 19, 2012 12:04
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



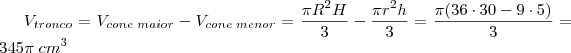




 , avisa que eu resolvo.
, avisa que eu resolvo.

