soluçao:
vamos tomar o primeiro quadrante para efeito de calculo,mas vale para qquer quadrante.
seja M(x,0) e N(0,y) os ponto dos eixos extremos do segmento que contem o ponto(a,b).
entao temos a seguinte configuraçao,vamos imaginar.uma reta inclinada,passando por (a,b),formando um triangulo retangulo com os eixos,onde o angulo reto seja a origem,ou seja o triang.retangulo MON.construamos dentro desse triang.retangulo o triangulo MbP,onde b,é o ponto (0,b) e P(a,b).esses triangulos sao semelhante,logo teremos as proporçoes:

daqui isolamos y=f(x),com algebrismos comuns(faça-os!),teremos:
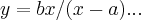
bom,sabemos que o segmento MN, é a hipotenusa do triangulo maior,MON,logo:
![MN=\sqrt[]{{x}^{2}+{y}^{2}}=\sqrt[]{{x}^{2}+{(bx/(x-a))}^{2}} MN=\sqrt[]{{x}^{2}+{y}^{2}}=\sqrt[]{{x}^{2}+{(bx/(x-a))}^{2}}](/latexrender/pictures/4868172b09e95c20d9da886cde048f09.png)
derivando MN,em relaçao a x, e igualando a zero,encontraremos o valor de x=f(a,b).esse sera o valor minimo ou valor maximo de MN.
verificaremos calculando a derivada segunda de MN,e verificando seu valor,que no caso deva ser positivo para qquer a e b,
mostrando ser ponto de minimo.entao aos interessados,termine-o...é calculo "pacas",mas compensa como exercicio e preparaçao...



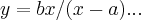
![MN=\sqrt[]{{x}^{2}+{y}^{2}}=\sqrt[]{{x}^{2}+{(bx/(x-a))}^{2}} MN=\sqrt[]{{x}^{2}+{y}^{2}}=\sqrt[]{{x}^{2}+{(bx/(x-a))}^{2}}](/latexrender/pictures/4868172b09e95c20d9da886cde048f09.png)





