Não consigo estabelecer um critério para calcular a altura do triangulo inscrito para daí calcular a sua área.
Sei somente que a resposta certa é a letra D porque, se considerar a altura do triangulo como o diâmetro da circunferência, o valor da área será 130 cm², mas como a altura é um pouquinho menor do que o diâmetro eu assinalei a opção D (125 cm²). Mas como calcular essa resposta com exatidão?
corresponde ao raio da circunferência, portanto, ele mede a metade do diâmetro;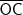
também é raio;
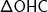é retângulo em 
;
.
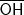![\sqrt[2]{144}](/latexrender/pictures/d86c95e7a1d45a5b6e7d0c89dd9a31b1.png "\sqrt[2]{144}")
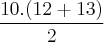
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)