Estou estudando para um processo seletivo do IFES, curso técnico. Para isso, tento resolver questões de anos anteriores, e empaquei na seguinte:

Não consigo visualizar a resolução de forma alguma!
Consegui apenas achar a altura do trapézio, depois de encontrar a altura do triângulo equilátero, de lado 6 (duas vezes o raio) formado pela conexão entre os centros de cada circunferência. Mas isso não me adiantou para encontrar o perímetro.
Alguma ajuda para encontrar os lados do quadrilátero e, assim, seu perímetro?
Grato!


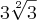 e
e 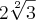 . Depois basta somar tudo e você chegará ao resultado
. Depois basta somar tudo e você chegará ao resultado 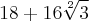

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)