[ângulos]

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[ângulos]

Regras do fórum
Responder

[ângulos]

Mensagempor Ederson_ederson » Qui Jul 02, 2015 08:49

Bom dia.

O ângulo alfa eu consegui encontrar e deu 20º.

Mas o ângulo BETA eu não sei exatamente por onde começar. Eu entendo que, se o ângulo adjacente ao beta (o que está logo abaixo dele) mede 40º pela semelhança de triângulos, o BETA deva medir 15º pelo mesmo motivo. Estou correto ou o BETA não tem a ver com a semelhança de triângulos e tem outra forma de fazer?

Obrigado! :y:
Anexos
quatão 20.jpg
Desenho do exercício
Ederson_ederson
Usuário Ativo
Usuário Ativo
 
Mensagens: 24
Registrado em: Ter Jun 23, 2015 19:04
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: [ângulos]

Mensagempor Baltuilhe » Qui Jul 02, 2015 12:39

Bom dia!

Veja se a minha solução está intelegível. Abraços!
yA1HaWYTFPfd79eKfCNaQM45.t1024u.jpg
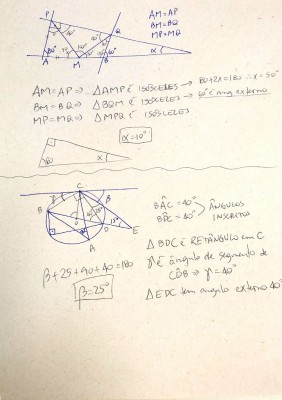
Solucao
Baltuilhe
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 60
Registrado em: Dom Mar 24, 2013 21:16
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Civil
Andamento: formado
Voltar ao topo

Re: [ângulos]

Mensagempor Ederson_ederson » Sáb Jul 04, 2015 11:25

Olá

Deu para entender sim.

Muito obrigado!
Ederson_ederson
Usuário Ativo
Usuário Ativo
 
Mensagens: 24
Registrado em: Ter Jun 23, 2015 19:04
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: [ângulos]

Mensagempor Ederson_ederson » Seg Jul 06, 2015 17:18

Baltuilhe escreveu:Bom dia!

Veja se a minha solução está intelegível. Abraços!
yA1HaWYTFPfd79eKfCNaQM45.t1024u.jpg


Olá... eu havia lido e entendido, mas tentei fazer novamente e me surgiu uma dúvida: como vc conseguiu achar o ângulo \gamma?

Não entendi quando vc colocou que ele é parte do segmento CÔB e por isso mede 40º. Por que ele mede 40º?

Obrigado :y:
Ederson_ederson
Usuário Ativo
Usuário Ativo
 
Mensagens: 24
Registrado em: Ter Jun 23, 2015 19:04
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo
Responder

Voltar para Geometria Plana

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum