E aqui... eu também estava em dúvida nessa:
Em um triângulo equilátero, ABE, cujo lado mede a , e um quadrado, BCDE, cujo lado também mede a. Com base nessas informações, é CORRETO afirmar que a área do triângulo
ABC é
a) a² / 3
b) a² / 4
c) a² ?3 / 4
d) a² ?3 / 4
No caso seria uma piramide quadrangular com os lados de valor a, então eu fiz da seguinte forma:
a = l² ?3 /4
a = a² ?3/4
Beleza, opção C, porém no gabarito diz ser opção B... alguem saberia me ajudar?



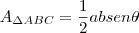



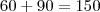 graus. E com isso sabemos os dois outros ângulos, já que é um triângulo isósceles: os ângulos A e C possuem 15 graus.
graus. E com isso sabemos os dois outros ângulos, já que é um triângulo isósceles: os ângulos A e C possuem 15 graus.

 um triângulo qualquer e
um triângulo qualquer e  sua altura. Sua área é definida como:
sua altura. Sua área é definida como: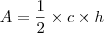
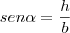
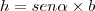
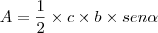
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)