[O anexo não pode ser exibido, pois a extensão pdf foi desativada pelo administrador.]



A figura sem escala mostra a planta de um calçadão no centro
de uma pequena cidade. Um pedestre, saindo de A, pode
chegar até B de duas formas distintas, ou seja, contornando
a praça triangular pela esquerda ou pela direita. Se o pedestre
caminhar por qualquer dos trajetos indicados pelas linhas
retas tracejadas, percorrerá a mesma distância em ambos os
casos. Os comprimentos de dois trechos retos dos trajetos são
dados na figura. Sabendo que a soma dos comprimentos x e y
dos trechos delimitados pelas setas na planta é igual a 12 m,
a razãopode ser expressa pela fração
 é a mesma coisa que andar
é a mesma coisa que andar  , logo podemos igualar as duas condições:
, logo podemos igualar as duas condições:
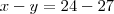
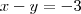 (equação 1)
(equação 1) (equação 2)
(equação 2)
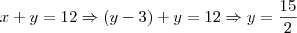

 é dado por:
é dado por:


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.