 por bruna106 » Dom Abr 20, 2008 22:07
por bruna106 » Dom Abr 20, 2008 22:07
Uma empresa de fornecimento de energia, ao instalar a rede elétrica numa fazenda precisou colocar dois postes em lados opostos de um lago para permitir a passagem da fiação, com isso surgiu um pequeno problema: para fazer o projeto da rede, seria necessário saber a distância entre os postes, e a presença do lago impedia a medição direta dessa distância.
Um dos engenheiros posicionou-se em um local onde era possível visualizar os dois postes e medir a distância entre eles.Com um aparelho apropriado, ele mediu o ângulo entre a linha de visão dele e os postes obtendo 120º.Um auxiliar mediu a distância do poste mais afastado do engenheiro e obteve 100 metros; Um outro auxiliar mediu o ângulo entre a linha do poste mais próximo do engenheiro e a linha entre os postes, obtendo 45º.Calcular a distância entre os postes.
Bom eu já conclui que o meio de se resolver esse problema é pela lei dos senos pois o problema nos informa dois ângulos.Não estou conseguindo desenhar e interpretar o problema já tentei e cheguei a duas possibilidades diferentes mas não sei se alguma delas esta correta:
Possibilidade1- 100/sen45º = x/sen15º
Possibilidade2- 100/sen45º = x/sen120º
Gostaria muito que alguém pudesse me ajudar e dizer se uma dessas possibilidades esta correta e se nenhuma delas estiver, me ajudar a resolve-lá de forma correta.
Obrigada
-
bruna106
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 20, 2008 21:47
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Dom Abr 20, 2008 23:10
por admin » Dom Abr 20, 2008 23:10
Olá Bruna, seja bem-vinda, boa noite!
Realmente, convém utilizar a lei dos senos.
A sua possibilidade 2 está correta, então considere o desenho relacionado.
Se precisar, posso enviar uma figura em seguida.
Obtive

metros de distância entre os postes.
Comente qualquer nova dúvida ou dificuldade.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por bruna106 » Dom Abr 20, 2008 23:46
por bruna106 » Dom Abr 20, 2008 23:46
Obrigada pela ajuda.
Seria ótimo que você me enviasse uma figura assim confiro com a minha e já tiro possíveis dúvidas quanto ao desenho.
Muitissímo obrigada
-
bruna106
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 20, 2008 21:47
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Abr 21, 2008 00:06
por admin » Seg Abr 21, 2008 00:06
A idéia é reduzir o problema para duas dimensões, considerando o plano do solo, as bases dos postes como dois pontos e a posição do engenheiro como o terceiro ponto do triângulo. Eis a figura:

- triangulo_postes.jpg (8.87 KiB) Exibido 11238 vezes
Espero ter ajudado!
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por bruna106 » Seg Abr 21, 2008 00:16
por bruna106 » Seg Abr 21, 2008 00:16
-
bruna106
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 20, 2008 21:47
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Abr 21, 2008 00:21
por admin » Seg Abr 21, 2008 00:21
Bruna, sua resolução está correta sim.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por bruna106 » Seg Abr 21, 2008 00:25
por bruna106 » Seg Abr 21, 2008 00:25
Muito obrigado pela ajuda.
Entendi perfeitamente como resolve-lo.
-
bruna106
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 20, 2008 21:47
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Abr 21, 2008 00:28
por admin » Seg Abr 21, 2008 00:28
OK Bruna, disponha do espaço.
E, obrigado por colaborar com as regras do fórum.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Me ajudem pois estou confuso...
por Fiel8 » Sáb Jun 27, 2009 18:41
- 4 Respostas
- 3129 Exibições
- Última mensagem por Fiel8

Sáb Jun 27, 2009 19:20
Funções
-
- [equação modular] resultado confuso
por jvabatista » Qua Abr 18, 2012 02:05
- 2 Respostas
- 1572 Exibições
- Última mensagem por jvabatista

Qua Abr 25, 2012 23:22
Álgebra Elementar
-
- DERIVADAS PARCIAIS, enunciado confuso
por inkz » Seg Nov 26, 2012 14:39
- 1 Respostas
- 2011 Exibições
- Última mensagem por MarceloFantini

Seg Nov 26, 2012 19:16
Cálculo: Limites, Derivadas e Integrais
-
- [Calcular XV dessa equação] ( Confuso !! )
por Andre Lopes » Sex Ago 30, 2013 13:08
- 0 Respostas
- 1064 Exibições
- Última mensagem por Andre Lopes

Sex Ago 30, 2013 13:08
Funções
-
- Circunferência e triângulo - Desde os dados já achei confuso
 por IsadoraLG » Ter Jul 08, 2014 19:38
por IsadoraLG » Ter Jul 08, 2014 19:38
- 1 Respostas
- 3409 Exibições
- Última mensagem por e8group

Ter Jul 08, 2014 20:51
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 metros de distância entre os postes.
metros de distância entre os postes.
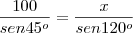
![\frac{100}{\frac{\sqrt[]{2}}{2}}= \frac{x}{\frac{\sqrt[]{3}}{2}} \frac{100}{\frac{\sqrt[]{2}}{2}}= \frac{x}{\frac{\sqrt[]{3}}{2}}](/latexrender/pictures/a582d641b9f63af863279e65a0ae1a35.png)
![\frac{x \sqrt[]{2}}{2}=\frac{100\sqrt[]{3}}{2} \frac{x \sqrt[]{2}}{2}=\frac{100\sqrt[]{3}}{2}](/latexrender/pictures/9a9b969fe1375ab225f73da6017fd0f5.png)
![x\frac{\sqrt[]{2}}{2}=50\sqrt[]{3} x\frac{\sqrt[]{2}}{2}=50\sqrt[]{3}](/latexrender/pictures/7266f41c68b18e748c132054698f230b.png)
![x\sqrt[]{2}=100\sqrt[]{3} x\sqrt[]{2}=100\sqrt[]{3}](/latexrender/pictures/a6ded96897b3cc3bc8193eca071e6560.png)
![x=\frac{100\sqrt[]{3}}{\sqrt[]{2}}.\frac{\sqrt[]{2}}{\sqrt[]{2}} x=\frac{100\sqrt[]{3}}{\sqrt[]{2}}.\frac{\sqrt[]{2}}{\sqrt[]{2}}](/latexrender/pictures/cec3993409663a124f2edcc91199fe9a.png)
![x=\frac{100\sqrt[]{6}}{2} x=\frac{100\sqrt[]{6}}{2}](/latexrender/pictures/5e205582d9afff70ba8c842314e83b07.png)
![x=50\sqrt[]{6} x=50\sqrt[]{6}](/latexrender/pictures/afca516928644548c201b6044e9529cc.png)
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
