FIz um concurso no domingo e tinha a seguinte questão:
Determinar a área de um triângulo equilátero cuja altura mede
![7\sqrt[]{3} 7\sqrt[]{3}](/latexrender/pictures/266244d554030a8cb7ca81936cdfd4f8.png) .
.a.
![49\sqrt[]{3} 49\sqrt[]{3}](/latexrender/pictures/bcdcb0c0f23b7a5a967953ffa9c6cdba.png) cm²
cm²b.
![\frac{27\sqrt[]{3}}{2} \frac{27\sqrt[]{3}}{2}](/latexrender/pictures/488bc12317aa5f7100c0e3a8661fd810.png) cm²
cm²c.
![\frac{49\sqrt[]{3}}{2} \frac{49\sqrt[]{3}}{2}](/latexrender/pictures/b431709f63cebffd6777f405e7aee15b.png) cm²
cm²d.
![36\sqrt[]{3} 36\sqrt[]{3}](/latexrender/pictures/da74fb0af9500edc47e48c3a673db4f5.png) cm²
cm²Minha conclusão foi:
-Se a área do triângulo é
 e o triângulo é equilátero ficamos com
e o triângulo é equilátero ficamos com ![\frac{{(7\sqrt[]{3})}^{2}}{2} \frac{{(7\sqrt[]{3})}^{2}}{2}](/latexrender/pictures/a44c7b958469d6cc4617545dc29138b3.png) , portanto, teríamos como resultado,
, portanto, teríamos como resultado, ![\frac{49\sqrt[]{3}}{2} \frac{49\sqrt[]{3}}{2}](/latexrender/pictures/b431709f63cebffd6777f405e7aee15b.png) .
.Porém, agora olhando no gabarito, verifiquei que a resposta certa seria LETRA:A então gostaria de pedir para que alguém me esclareça: Estou errado ou o gabarito é que está incorreto?
Desde já agradeço a ajuda.
Bruno


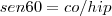 .
.![sen 60 = \frac{7\sqrt[]{3}}{a} sen 60 = \frac{7\sqrt[]{3}}{a}](/latexrender/pictures/4ed9f2b42ccff8a0963bbe5834f8d620.png) , como
, como ![sen 60 = \sqrt[]{3}/2 sen 60 = \sqrt[]{3}/2](/latexrender/pictures/b88fc0d9d332c9504862bbb60e0027d8.png) temos:
temos: ![\sqrt[]{3}/2 = 7\sqrt[]{3}/a \sqrt[]{3}/2 = 7\sqrt[]{3}/a](/latexrender/pictures/3f5f2e3bbca928424abcacc6e03895cc.png) . Multiplicando em cruz:
. Multiplicando em cruz: ![a.\sqrt[]{3} = 14.\sqrt[]{3} a.\sqrt[]{3} = 14.\sqrt[]{3}](/latexrender/pictures/4f53b0ec7569603e22069a7188f40cf2.png) . Portanto, a = 14.
. Portanto, a = 14.![\frac{14.7\sqrt[]{3}}{2} \frac{14.7\sqrt[]{3}}{2}](/latexrender/pictures/09c533e8ce6b83683d8f6ecca445d95f.png) =
= ![49\sqrt[]{3}{cm}^{2} 49\sqrt[]{3}{cm}^{2}](/latexrender/pictures/6875ea3448e972b13c40b1a1c9a5dbf4.png) .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.