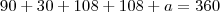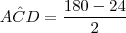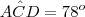por Gustavo Gomes » Sex Jan 31, 2014 21:50
Olá, Pessoal!
Na figura a seguir, o triângulo equilátero ABC e o pentágono regular ADEFG possuem lados de mesmo comprimento e estão em posição tal que as retas BC e GF são paralelas.
Quanto mede o ângulo ACD?
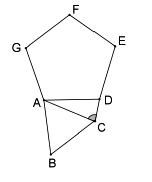
- imagem.PNG (4.4 KiB) Exibido 2968 vezes
A resposta é 78º.
Considerei a medida dos ângulos internos do pentágono regular e do Triângulo equilátero; tentei prolongar os segmentos AC e GF e trabalhar com ângulos complementares e opostos pelo vértice, mas não consegui chegar no resultado.
Aguardo, grato.
-
Gustavo Gomes
- Usuário Parceiro
-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
por young_jedi » Ter Fev 18, 2014 12:24
- equilateros.png (5.38 KiB) Exibido 2924 vezes
como as retas são paralelas então podemos traçar uma reta perpendicular com angulo de 90º com ambas
como o angulo do triangulo é 60º então ao angulo entre as retas GC e CA é 30º
então pela soma dos angulos internos do quadrilatero temos
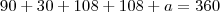
como o trianulo ACD é isoceles pois possui dois lados inguais então
-
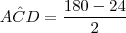
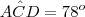
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida - Medida do ângulo
por flaviano » Dom Nov 07, 2010 12:30
- 6 Respostas
- 4386 Exibições
- Última mensagem por Jefferson
Dom Nov 28, 2010 23:22
Geometria Plana
-
- Determine a medida do ângulo
por andersontricordiano » Ter Jun 07, 2011 14:19
- 1 Respostas
- 2377 Exibições
- Última mensagem por Molina
Seg Jun 13, 2011 02:08
Geometria
-
- Expressar medida do ângulo em radianos e graus?
por FilipiM » Dom Mar 09, 2014 16:54
- 1 Respostas
- 2253 Exibições
- Última mensagem por Russman
Dom Mar 09, 2014 23:57
Trigonometria
-
- Calcule a medida do ângulo BNP formado dentro do losango
por andersontricordiano » Ter Abr 05, 2011 19:07
- 1 Respostas
- 4606 Exibições
- Última mensagem por Elcioschin
Ter Abr 05, 2011 19:28
Geometria
-
- Sistema de medida - medida de área
por Igra » Qui Abr 11, 2013 09:53
- 2 Respostas
- 4741 Exibições
- Última mensagem por Igra
Sex Abr 12, 2013 19:37
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
