geometria

por **zenildo** » Dom Mai 05, 2013 19:59

Um ciclista de uma prova de resistencia deve percorrer 500km sobre uma pista circular de raio 200m. O número aproximadfo de voltas que ele deve dar é:

a) 100
b) 200
c) 300
d)400
e)500

por **natanaelskt** » Dom Mai 05, 2013 23:21

boa noite.
o raio da pista é 200m. o comprimento da circunferência é C=2rR
logo> C= 2x3,14x200=1256
para saber o número de voltas divide a distançia a ser percorrida pelo comprimento da circundefência.
assim.
500Km/1256m
passa Km para m
500000/1256 = 398.08 voltas . quase 400 voltas

por **Luis Gustavo** » Seg Mai 06, 2013 15:57

Só complementando a resposta do amigo aí em cima.

O comprimento de uma circunferência é dado pela seguinte fórmula:
$2\pi r$
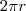
Onde é o raio da circunferência, no nosso caso 200m e $\pi$ (lê-se pi) é uma constante matemática pertencente ao conjunto dos irracionais, que nós vamos abreviar como $\pi=3,14.$ Então, vamos calcular o comprimento da circunferência.

$C=2\times\pi\times200$
$C=400\times\pi$
$C=400\times3,14$

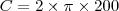
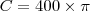
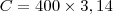
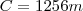
Note que este valor não é exato, pois usamos um valor aproximado para $\pi$ . Cada volta completa na pista corresponde a 1256m. Queremos saber quantas voltas é preciso dar para completar 500km. Primeiro transformamos 500km em metros:

$500 \times 1000$

E agora só falta dividir a distancia que o ciclista deve percorrer pelo comprimento da pista.

$\dfrac{500000}{1256} \cong 398,08$ voltas.

E o valor aproximado que obtemos é 398,08; o que significa que o número aproximado de voltas que o ciclista deve dar é aproximadamente 400.

Resposta: d) 400.

Espero ter ajudado.
Att, Luis Gustavo.

geometria

geometria

geometria

Re: geometria

Re: geometria

Quem está online