 por _Jane » Sex Abr 05, 2013 15:56
por _Jane » Sex Abr 05, 2013 15:56
Mostre que se dois ângulos de um triangulo são congruentes, então o triangulo é isósceles.
Considerei dois triangulos congruentes, mas não consigo sair dessa parte!
-
_Jane
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 05, 2013 15:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por e8group » Sex Abr 05, 2013 17:54
por e8group » Sex Abr 05, 2013 17:54
Segue uma resolução elementar ...
Considere o triângulo

e

,

ângulos distintos interno do triângulo tais que

e
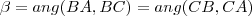
.Suponha que

seja um ponto pertence à reta

tal que

.
Desta forma ,por relações trigonométricas ,segue
(i)
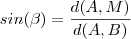
(ii)
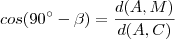
.
De
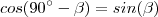
e (i) + (ii) resulta que

.
A última etapa é mostrar que

.Utilize o fato que
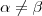
. Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por _Jane » Sáb Abr 06, 2013 00:48
por _Jane » Sáb Abr 06, 2013 00:48
Muito Obrigada! Vou tentar finalizar!
-
_Jane
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 05, 2013 15:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Euclidiana
por Caeros » Seg Mai 25, 2009 19:13
- 1 Respostas
- 2015 Exibições
- Última mensagem por Caeros

Seg Mai 25, 2009 19:33
Geometria Plana
-
- Geometria Euclidiana
por rheilagouveia » Sex Mai 21, 2010 02:25
- 1 Respostas
- 3581 Exibições
- Última mensagem por MarceloFantini

Sex Mai 21, 2010 14:15
Apresentação dos Participantes
-
- AXIOMAS Geometria Euclidiana
por JullyanaErwitz » Qui Mai 05, 2011 01:32
- 0 Respostas
- 1324 Exibições
- Última mensagem por JullyanaErwitz

Qui Mai 05, 2011 01:32
Geometria Plana
-
- geometria euclidiana plana
por daniela1994 » Ter Mar 13, 2012 15:47
- 2 Respostas
- 2617 Exibições
- Última mensagem por Luiz Augusto Prado

Qua Mar 14, 2012 08:30
Geometria Plana
-
- [Geometria Euclidiana Plana]
por Pessoa Estranha » Qua Ago 07, 2013 18:05
- 1 Respostas
- 2056 Exibições
- Última mensagem por e8group

Qui Ago 08, 2013 16:23
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e  ,
,  ângulos distintos interno do triângulo tais que
ângulos distintos interno do triângulo tais que  e
e 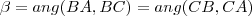 .Suponha que
.Suponha que  seja um ponto pertence à reta
seja um ponto pertence à reta  tal que
tal que  .
. 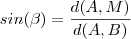
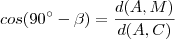 .
. 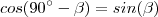 e (i) + (ii) resulta que
e (i) + (ii) resulta que  .
.  .Utilize o fato que
.Utilize o fato que 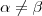 . Tente concluir .
. Tente concluir .
