 por fernandocez » Sex Nov 23, 2012 15:54
por fernandocez » Sex Nov 23, 2012 15:54
Mais uma questão que não consegui resolver.
49) Os pontos A(1,3), B(4,0) e C(3, k) são vértices de um triângulo retângulo, onde o ângulo CÂB é reto, e k é um número real. A hipotenusa desse triângulo mede:
a)
![\sqrt[]{13} \sqrt[]{13}](/latexrender/pictures/2e90750460e35e2d0642549705d5a7c8.png)
b)
![2\,\sqrt[]{13} 2\,\sqrt[]{13}](/latexrender/pictures/813a977b81d91e4cf6991c75efc0f8cf.png)
c)
![\sqrt[]{26} \sqrt[]{26}](/latexrender/pictures/600cdd78b650c67c223dff983b7e7d6f.png)
(resposta certa)
d)
![2\,\sqrt[]{26} 2\,\sqrt[]{26}](/latexrender/pictures/e81adc87466012c051833a47a38a2cc6.png)
e)
![3\,\sqrt[]{26} 3\,\sqrt[]{26}](/latexrender/pictures/dc96338b211d2e4a9f00db01738d04d2.png)

Eu fiz o desenho me baseando na possibilidade da coordenada C ser (3, 5). Primeiro tentei encontrar o "K" com as fórmulas de geometria analítica (distancia entre dois pontos, e etc) e não consegui. Se tivesse conseguido, ai sim usaria a geom. analitica pra encontrar o tamanho da hipotenusa. Agradeço quem puder me orientar a melhor forma de resolve o problema.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por young_jedi » Sex Nov 23, 2012 17:33
por young_jedi » Sex Nov 23, 2012 17:33
voce encontrou que k é igual a 5 esta certo
oque voce tem que fazer e traçar uma reta que vai do ponto C(3,5) ate o ponto (3,0) e uma reta de (3,0) ate o ponto B (4,0) então voce tera um triangulo retangulo em que um cateto mede 5 e o outro mede 1 portanto por pitagoras
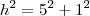

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por fernandocez » Sex Nov 23, 2012 19:38
por fernandocez » Sex Nov 23, 2012 19:38
A segunda parte ficou clara. Mas eu não encontrei o valor de K, eu fui na tentativa até encontrar o k = 5. Gostaria de saber como encontrar o valor de K de forma correta. Agradeço pela ajuda Young_jed.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por young_jedi » Sex Nov 23, 2012 21:31
por young_jedi » Sex Nov 23, 2012 21:31
A sim tranquilo fernandocez
trace uma reta paralela ao eixo y e que passe pelo ponto A

- QUESTO~1.JPG (19.69 KiB) Exibido 3559 vezes
por semelhança de triangulos
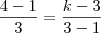


-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por fernandocez » Sáb Nov 24, 2012 16:17
por fernandocez » Sáb Nov 24, 2012 16:17
Valeu mesmo!! Eu não conseguia ver esses dois outros triângulos e pensei que só dava pra resolver por geometria analítica. Era muito mais fácil que eu imaginava. Mais uma vez obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria plana] questão concurso 2011
por fernandocez » Sáb Out 08, 2011 00:25
- 3 Respostas
- 4696 Exibições
- Última mensagem por fernandocez

Sex Mar 16, 2012 22:51
Geometria Plana
-
- [equações lineares] Concurso magistério 03/2011
por fernandocez » Qui Jul 19, 2012 19:14
- 4 Respostas
- 3375 Exibições
- Última mensagem por fraol

Sex Jul 20, 2012 20:49
Sistemas de Equações
-
- Questão prova magisterio 2008
por fernandocez » Seg Fev 14, 2011 16:42
- 4 Respostas
- 3031 Exibições
- Última mensagem por LuizAquino

Ter Fev 15, 2011 20:10
Polinômios
-
- Questão prova magisterio 2007
 por fernandocez » Seg Fev 14, 2011 17:21
por fernandocez » Seg Fev 14, 2011 17:21
- 1 Respostas
- 1417 Exibições
- Última mensagem por LuizAquino

Seg Fev 14, 2011 19:57
Geometria Plana
-
- Questão prova magisterio 2008
 por fernandocez » Sáb Fev 26, 2011 11:39
por fernandocez » Sáb Fev 26, 2011 11:39
- 3 Respostas
- 2396 Exibições
- Última mensagem por LuizAquino

Sáb Fev 26, 2011 19:15
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{13} \sqrt[]{13}](/latexrender/pictures/2e90750460e35e2d0642549705d5a7c8.png)
![2\,\sqrt[]{13} 2\,\sqrt[]{13}](/latexrender/pictures/813a977b81d91e4cf6991c75efc0f8cf.png)
![\sqrt[]{26} \sqrt[]{26}](/latexrender/pictures/600cdd78b650c67c223dff983b7e7d6f.png) (resposta certa)
(resposta certa)![2\,\sqrt[]{26} 2\,\sqrt[]{26}](/latexrender/pictures/e81adc87466012c051833a47a38a2cc6.png)
![3\,\sqrt[]{26} 3\,\sqrt[]{26}](/latexrender/pictures/dc96338b211d2e4a9f00db01738d04d2.png)



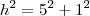

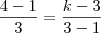


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.