36. Em um terreno retangular, como mostra a figura abaixo, foi construída uma oficina de formato triangular (triângulo retângulo). O polinômio que expressa a área não construída (escura) deste terreno é:
a) 20 x² + 12x
b) 20 x² + 8x
c) 20 x² + 16x
d) 25x² + 12x
e)
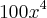 +
+

Eu calculei a área total
At = (5x + 4)4x = 20x² + 16x
faltou calcular a área do triângulo (polinômio) para subtrair da área total.
Marquei mas alguns valores na figura mas não consegui evoluir disso. A resposta certa é: (a)
Agradeço quem puder ajudar.


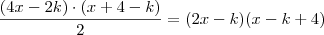 . Com o valor de
. Com o valor de  , que é este comprimento, você substitui e encontrará o outro polinômio, bastando subtrair da área total.
, que é este comprimento, você substitui e encontrará o outro polinômio, bastando subtrair da área total.

 .
. 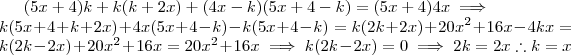 .
.  .
. 
 .
.
 :
: