 por fernandocez » Sáb Out 20, 2012 14:47
por fernandocez » Sáb Out 20, 2012 14:47
Questão 37 (Concurso Bombeiro RJ 2008)
Na figura abaixo, o triângulo ABC é equilátero com AM = MB = 4 cm e CD = 6 cm.

A área do triângulo CDE, em cm², é:
Alternativa certa:
A)
![\frac{18\sqrt[]{3}}{5} \frac{18\sqrt[]{3}}{5}](/latexrender/pictures/01d8b44244309325896e5af01a521759.png)
Eu tentei encontrar uma semelhança entre os dois triângulos de baixo, mas só tem um angulo congruente.
Outra dúvida se eu tiver as medidas do triangulo CDE, como encontro a área desse triãngulo? Pela formula Bxh/2 teria que ter a altura (h), certo! Aguardo ajuda, obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por young_jedi » Sáb Out 20, 2012 15:55
por young_jedi » Sáb Out 20, 2012 15:55
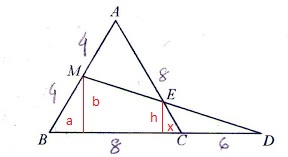
- figura triangulo.jpg (9.96 KiB) Exibido 5555 vezes
levando em consideração que é um triangulo equilatero então sabemos que os angulos em A, B e C medem 60º
com isso temos


e
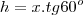

por semelhança de triangulos

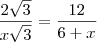
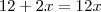
resolvendo encontra-se x e com isso h, depois é so utilizar o calculo da area
Se voce tivesse as medidas dos lados do triangulo, voce teria que calcular a altura relativa a um dos lados para calcular a area.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por fernandocez » Sáb Out 20, 2012 21:13
por fernandocez » Sáb Out 20, 2012 21:13
Obrigado young_jedi pela ajuda. Vou transferir para o caderno e estudar essa resolução. Um abração.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analitica] Area de triangulo
por LucasSG » Sex Jun 21, 2013 10:57
- 1 Respostas
- 1513 Exibições
- Última mensagem por young_jedi

Sex Jun 21, 2013 21:23
Geometria Analítica
-
- geometria analitica (área do triângulo)
por romarioharket » Qua Nov 13, 2013 00:01
- 1 Respostas
- 3332 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 11:28
Geometria Analítica
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4414 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\frac{18\sqrt[]{3}}{5} \frac{18\sqrt[]{3}}{5}](/latexrender/pictures/01d8b44244309325896e5af01a521759.png)




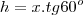


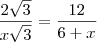
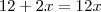


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.