 por Malorientado » Seg Ago 06, 2012 23:51
por Malorientado » Seg Ago 06, 2012 23:51
Uma placa de alumínio tem a forma de um paralelograma. Suas medidas estão indicadas na figura(Na figura, há um paralelograma de base 40cm e lado 25 cm, o seu ângulo inferior da direita é 120°). Calcule a área dessa placa. Dúvida: Posso achar a área por base . lado? Seria a mesma coisa de um retângulo de base 40 e lado 25, não seria?
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Ago 07, 2012 03:23
por MarceloFantini » Ter Ago 07, 2012 03:23
Não exatamente. Você precisa encontrar a altura do lado relativo à base. Num retângulo isto coincide, não é o caso do paralelogramo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Malorientado » Sex Ago 10, 2012 22:48
por Malorientado » Sex Ago 10, 2012 22:48
Achando a área do paralelograma por 2 vezes a área do triângulo de lados 40 e 25cm e ângulo 120°, em

, obtive 580cm², é isso? Bom não sei porque não consegui resolver esse exercício encontrando a altura do paralelograma pelo cosseno de 30°(subindo uma reta em 90° no ângulo de 120°, sobra um ângulo de 30°,correto?) fiz cos 30°= 0,154=

, altura= 25 . 0,154= 3,85,

. Onde errei?
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sex Ago 10, 2012 23:47
por MarceloFantini » Sex Ago 10, 2012 23:47
Você está com valores errados, note que
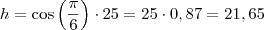
e daí a área seria
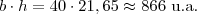
.
Ou seja,

e não 0,153.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Malorientado » Sex Ago 10, 2012 23:58
por Malorientado » Sex Ago 10, 2012 23:58
O valor para cos 30°peguei da net, maldita... Então do primeiro jeito que fiz obtive 580cm² e desse outro, 866cm². Qual das duas respostas está correta? Qual o erro da incorreta?
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Ago 11, 2012 00:26
por MarceloFantini » Sáb Ago 11, 2012 00:26
A área de um paralelogramo é base vezes altura, logo

, onde você pode escrever a altura em função do outro lado usando trigonometria. Note que a sua expressão não é coerente pois você ainda divide por dois.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Malorientado » Sáb Ago 11, 2012 01:00
por Malorientado » Sáb Ago 11, 2012 01:00
Na primeira tentativa de resolução, como não tinha a altura, resolvi achar a área do triângulo de lados 40 e 25cm e ângulo 120° pela fórmula

. Encontrando essa área, bastaria multiplicar por 2, pois o paralelograma é = a 2 triângulos. Não é isso?
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Ago 11, 2012 01:09
por MarceloFantini » Sáb Ago 11, 2012 01:09
Realmente, o método está correto porém você deve ter errado o valor do seno. O resultado será o mesmo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Malorientado » Sáb Ago 11, 2012 01:18
por Malorientado » Sáb Ago 11, 2012 01:18
Maldito google, olha o quanto nos atrasou? O valor que ele retorna para sen 120 = 0,580611184...
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Ago 11, 2012 01:25
por MarceloFantini » Sáb Ago 11, 2012 01:25
O google está programado para aceitar o valor em radianos, não em graus. O equívoco na verdade foi seu.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4419 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 2132 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2903 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Area
por karenblond » Qui Mar 25, 2010 17:19
- 6 Respostas
- 4172 Exibições
- Última mensagem por Molina

Ter Mar 30, 2010 00:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 , obtive 580cm², é isso? Bom não sei porque não consegui resolver esse exercício encontrando a altura do paralelograma pelo cosseno de 30°(subindo uma reta em 90° no ângulo de 120°, sobra um ângulo de 30°,correto?) fiz cos 30°= 0,154=
, obtive 580cm², é isso? Bom não sei porque não consegui resolver esse exercício encontrando a altura do paralelograma pelo cosseno de 30°(subindo uma reta em 90° no ângulo de 120°, sobra um ângulo de 30°,correto?) fiz cos 30°= 0,154=  , altura= 25 . 0,154= 3,85,
, altura= 25 . 0,154= 3,85,  . Onde errei?
. Onde errei?
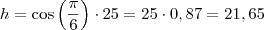 e daí a área seria
e daí a área seria 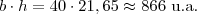 .
. e não 0,153.
e não 0,153.


 , onde você pode escrever a altura em função do outro lado usando trigonometria. Note que a sua expressão não é coerente pois você ainda divide por dois.
, onde você pode escrever a altura em função do outro lado usando trigonometria. Note que a sua expressão não é coerente pois você ainda divide por dois.

 . Encontrando essa área, bastaria multiplicar por 2, pois o paralelograma é = a 2 triângulos. Não é isso?
. Encontrando essa área, bastaria multiplicar por 2, pois o paralelograma é = a 2 triângulos. Não é isso?






 .
.



