 por Paula Caroline » Dom Mai 06, 2012 21:48
por Paula Caroline » Dom Mai 06, 2012 21:48
A superfície de uma certa masa é um quadrado, composto de quatro triângulos isósceles congruentes cujos lados congruentes medem
![\frac{3\sqrt[2]{2}}{5} \frac{3\sqrt[2]{2}}{5}](/latexrender/pictures/ac13644a6d1a3b548647e4ab00ac56e3.png)
m.
Determine a área de superfície dessa mesa.
-
Paula Caroline
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 06, 2012 20:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Walter Clack » Dom Mai 06, 2012 22:31
por Walter Clack » Dom Mai 06, 2012 22:31
Se vc desenhar um quadrado e dividi-lo traçando suas duas diagonais vc terá 4 triângulos isósceles congruentes.
Como cada triângulo tem dois lados congruentes ( menos o da base do triângulo) então qualquer uma das diagonais do quadrado vai ser a soma de um lado do triângulo com um lado do outro triângulo .( tipo assim o lado esquero do triangulo de baixo mais o lado direito do triângulo de cima) .
Como os lados congruentes de cada triângulo mede
![\frac{3\sqrt[2]{2}}{5} \frac{3\sqrt[2]{2}}{5}](/latexrender/pictures/ac13644a6d1a3b548647e4ab00ac56e3.png)
Usando o teorema de pitágoras para achar o lado do quadrado temos.
![{l}^{2}+{l}^{2}={\frac{3\sqrt[2]{2}}{5}}^{2} {l}^{2}+{l}^{2}={\frac{3\sqrt[2]{2}}{5}}^{2}](/latexrender/pictures/aa3e78bc92d39aa76c4d7c6b62aee91e.png)

que resulta

não precisamos calcular a raíz quadrada pois a área do quadrado é dado por

com l representando o lado
logo a área é

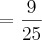
-
Walter Clack
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 06, 2012 22:04
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática Bacharelado
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Áreas de superfícies planas
por andersontricordiano » Dom Mar 13, 2011 02:34
- 1 Respostas
- 3043 Exibições
- Última mensagem por MarceloFantini

Dom Mar 13, 2011 03:53
Geometria
-
- Conjunto de Figuras Planas
por gustavowelp » Qua Jun 30, 2010 15:37
- 4 Respostas
- 4344 Exibições
- Última mensagem por gustavowelp

Qua Jun 30, 2010 17:44
Álgebra Elementar
-
- Geometria (área de figuras planas
 por claudia » Sex Out 31, 2008 00:19
por claudia » Sex Out 31, 2008 00:19
- 1 Respostas
- 6537 Exibições
- Última mensagem por admin

Sáb Nov 01, 2008 13:09
Geometria Plana
-
- Superfícies cilindricas
por Priscila_moraes » Qua Nov 16, 2011 12:23
- 0 Respostas
- 1204 Exibições
- Última mensagem por Priscila_moraes

Qua Nov 16, 2011 12:23
Geometria Analítica
-
- [Superfícies e Planos] Interseção
por pedrolinhares » Dom Jun 18, 2017 18:22
- 0 Respostas
- 1806 Exibições
- Última mensagem por pedrolinhares

Dom Jun 18, 2017 18:22
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{3\sqrt[2]{2}}{5} \frac{3\sqrt[2]{2}}{5}](/latexrender/pictures/ac13644a6d1a3b548647e4ab00ac56e3.png) m.
m.
![\frac{3\sqrt[2]{2}}{5} \frac{3\sqrt[2]{2}}{5}](/latexrender/pictures/ac13644a6d1a3b548647e4ab00ac56e3.png) m.
m.
![\frac{3\sqrt[2]{2}}{5} \frac{3\sqrt[2]{2}}{5}](/latexrender/pictures/ac13644a6d1a3b548647e4ab00ac56e3.png)
![{l}^{2}+{l}^{2}={\frac{3\sqrt[2]{2}}{5}}^{2} {l}^{2}+{l}^{2}={\frac{3\sqrt[2]{2}}{5}}^{2}](/latexrender/pictures/aa3e78bc92d39aa76c4d7c6b62aee91e.png)


 com l representando o lado
com l representando o lado
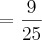

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
