 por DanielRJ » Dom Dez 18, 2011 13:22
por DanielRJ » Dom Dez 18, 2011 13:22
Olá depois de muito tempo to de volta.
To com duvida nesta questão fiquei nela na prova da Pm-Es:
Luana desenhou em seu caderno o triangulo ABC, cujas medidas B=70º e A=40º o lado BC mede 12,8. A área oupada por esse triangulo é de aproximadamente :
Dados : sen40º=0,64 ; cos40º=0,76; sen70º=0,94 ; cos70º=0,34.Resposta : 120 cm²
Minha resolução:
Usando a lei dos senos temos:
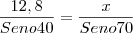
Aqui eu achei os lados :
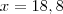
Agora no calculo da area que estou me enrolando!
- Anexos
-
- Questão80.jpg (10.3 KiB) Exibido 1777 vezes
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Dom Dez 18, 2011 15:33
por DanielRJ » Dom Dez 18, 2011 15:33
Amigos consegui resolver a questão . Foi muita falta de atenção peço desculpas
Mas a Questão fica ai pra tirar a duvida de alguem:
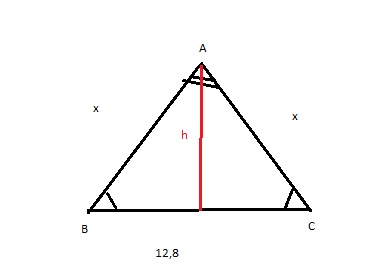
Resolução :
Sendo : h = 18,8 e b= 12,8
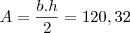
cm

-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações Métricas
por janderson77 » Seg Dez 02, 2013 12:28
- 0 Respostas
- 942 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:28
Geometria Plana
-
- Demonstração Relações Métricas
 por PedroSantos » Ter Dez 07, 2010 22:59
por PedroSantos » Ter Dez 07, 2010 22:59
- 1 Respostas
- 1761 Exibições
- Última mensagem por VtinxD

Dom Dez 12, 2010 22:23
Trigonometria
-
- relaçoes metricas nos triangulos
por stanley tiago » Sáb Fev 12, 2011 19:34
- 4 Respostas
- 2830 Exibições
- Última mensagem por stanley tiago

Dom Fev 13, 2011 18:04
Geometria Plana
-
- relaçoes metricas na circuferencia
 por stanley tiago » Seg Abr 11, 2011 18:37
por stanley tiago » Seg Abr 11, 2011 18:37
- 2 Respostas
- 2000 Exibições
- Última mensagem por stanley tiago

Ter Abr 12, 2011 10:06
Geometria Analítica
-
- Circunferencia e relações metricas
 por alfabeta » Qua Fev 29, 2012 00:09
por alfabeta » Qua Fev 29, 2012 00:09
- 0 Respostas
- 1688 Exibições
- Última mensagem por alfabeta

Qua Fev 29, 2012 00:09
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
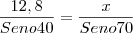
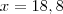


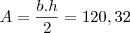 cm
cm


 , avisa que eu resolvo.
, avisa que eu resolvo.

