 o Colégio Pedro II 6o ano
o Colégio Pedro II 6o anoUma costureira, sem saber, comprou certo tecido que encolheu, ao ser molhado, 1/11 do comprimento e 1/12 da largura. A largura original era 1,5 m. Quantos metros desse tecido devemos comprar para, depois de molhado, obter 75 m quadrado?
Bom dia!!!!
Aos queridos colaboradores, gostaría que me ajudassem a entender o enunciado do problema. Acredito que esteja mal formulado. O meu raciocínio foi que, A costureira comprou um tecido e molhou, quando mollhou ele encolheu e agora ela precisa comprar mais tecido para chegar a 75 metro quadrado.
Meus cálculos:
-COMPRIMENTO 11/11 ( comprimento = incógnita), vamos chamar de x;
-encolheu 1/11 do comprimento
-LARGURA 12/12 = 1,5 m
-1/12 de 1,5 = 0,125 m ( encolheu)
-largura encolhida = 1,5 - 0,125 = 1,375 m
-ÁREA = 75 metro quadrado
CALCULANDO A ÁREA DO TECIDO ANTES DE ENCOLHER:
A = Comprimento x largura
Substituindo:
c. l = A
X . 1,5 = 75
X = 75 / 1,5
X = 50 , ou seja o comprimento do tecido antes de encolher é igual a 50m
Substituindo:
- comprimento 11/11 = 50
- 1/11 de 50 = 4,54 ( encolheu) ( considerando duas casa decimais apos à vírgula)
- comprimento encolhido = 50 - 4,54 = 45,46
Calculando novamente a área com todas as medidas encolhidas:
A = comprimento x largura
A = 45,46 x 1,375
A = 62,50 metro quadrado
A costureira ficou com 62,50 metro quadrado e para chegar a 75 metro quadrado ela precisa comprar; e não nós:
75 - 62,50 = 12,50 metro quadrado.
PARA ENCONTRAR QUANTOS METROS DE COMPRIMENTO A COSTUREIRA DEVE COMPRAR, CONSIDERANDO A MESMA LARGURA DO TECIDO ENCOLHIDO: ( já que o enunciado dizia depois de molhado)
A = 12,50 metros quadrado
largura = 1,375
comprimento = x
Substituindo:
A = c. l
x . 1,375 = 12,50
x = 12,50 / 1,375
x = 9,09
PROVA REAL COMPRIMENTO LARGURA ÁREA
medidas do tecido seco 50m x 1,5 m = 75 metro quadado
medidas do tecido molhado 45,46m x 1,375m = 62,50 metro quadrado
nova compra do tecido 9,09 x 1,375m = 12,50 metro quadrado
AS NOVAS MEDIDAS DO TECIDO DA COSTUREIRA SÃO:
COMPRIMENTO LARGURA ÁREA
o tecido molhado que sobrou 45,46m x 1,375 m = 62,50 metro quadrado
nova compra do tecido 9,09m x 1,375 m = 12,50 metro quadado
TOTAL MEDIDA COMPRIMENTO 54,55 X 1,375m = 75 metro quadrado


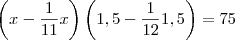

 Muito obrigada Luiz Aquino, pelo esclarecimento. Se ficou difícil para mim, imagina para as crianças, oriundas de escola Pública que agora estudam no Pedro II ?
Muito obrigada Luiz Aquino, pelo esclarecimento. Se ficou difícil para mim, imagina para as crianças, oriundas de escola Pública que agora estudam no Pedro II ?  É um grande equívoco um professor passar um problema desta natureza para o 6o. ano, quando eles ainda nem aprenderam equação de 1o grau. E sequer foi passado a eles em aula ao menos um problema parecido. Só nos resta, pedirmos esclarecimentos perante a Instituição. Afinal são nossos filhos e de maneira alguma devemos permitir que se sintam humilhados diante às dificuldades que estão encontrando em matemática.
É um grande equívoco um professor passar um problema desta natureza para o 6o. ano, quando eles ainda nem aprenderam equação de 1o grau. E sequer foi passado a eles em aula ao menos um problema parecido. Só nos resta, pedirmos esclarecimentos perante a Instituição. Afinal são nossos filhos e de maneira alguma devemos permitir que se sintam humilhados diante às dificuldades que estão encontrando em matemática.