por Gustavo R » Sex Ago 12, 2011 21:06
por Gustavo R » Sex Ago 12, 2011 21:06
(ESAL) Seja AB tal que AB = a e AM/MB = 3/5. A posição relativa de M é dada pela relação:
a) Am = 3/8 de a
b) AM = 8/3 de a
c) Am = 5/8 de a
d) AM = 8/5 de a
Oi galera, eu estou tendo dúvidas para resolver esta questão... pelo fato de eu ñ ter conseguido interpretá-la, eu ñ desenvolvi o cálculo ainda. Se alguém puder me dar uma força com ela, por favor me explique o raciocínio. Obrigado!
-
Gustavo R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 12, 2011 19:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Guill » Sáb Ago 13, 2011 10:26
por Guill » Sáb Ago 13, 2011 10:26
AB é um segmento de reta de valor a. O ponto M divide a reta AB em dois outros segmentos AM e MB de tal forma que:

Dessa relação, dedusimos que:
5.AM = 3.MB
Mas sabemos que AM + MB = AB
Através de um sistema:
{5.AM - 3.MB = 0
{AM + MB = a
{5.AM - 3.MB = 0
{AM + MB = a (3)
{5.AM - 3.MB = 0
{3.AM + 3.MB = 3a
8.AM = 3a
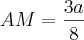
A resposta é a letra a
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Gustavo R » Sáb Ago 13, 2011 14:49
por Gustavo R » Sáb Ago 13, 2011 14:49
entendi cara, muito obrigado!... mas só me responde uma coisa: qual foi o ponto principal ao longo da resolução, que te ajudou a enxergar esse sistema? e pelo gabarito a resposta é mesmo A. Valew e até mais!
-
Gustavo R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 12, 2011 19:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFC) Seja f a função...
por manuoliveira » Sex Ago 27, 2010 22:20
- 2 Respostas
- 1993 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 28, 2010 17:03
Funções
-
- Seja ?(x) uma função derivavel
por kak9 » Ter Out 02, 2018 15:33
- 0 Respostas
- 2975 Exibições
- Última mensagem por kak9

Ter Out 02, 2018 15:33
Cálculo: Limites, Derivadas e Integrais
-
- P.A -Seja ABC um triangulo retangulo
por CrescentMurr » Dom Mar 17, 2013 19:40
- 1 Respostas
- 1763 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:19
Progressões
-
- [Limites] Seja f(x) = (3x - 2)/(x - 2) RESOLVIDO
por yuricastilho » Sáb Abr 05, 2014 19:59
- 3 Respostas
- 1609 Exibições
- Última mensagem por yuricastilho

Dom Abr 06, 2014 22:45
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Seja f: R -> R responda:
por yuricastilho » Qui Abr 10, 2014 00:15
- 2 Respostas
- 4833 Exibições
- Última mensagem por yuricastilho

Ter Abr 15, 2014 14:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.