Boa noite!
Necessito de um auxílio urgente nessa questão. Meu prof. já afirmou que ela cairá na prova na qual preciso recuperar nota.
Calcular o raio da base de uma lata de cerveja cilindrica de capacidade igual a 0,5 litros, de modo que o material gasto na lata seja mínimo.
Eis o que eu fiz:
500 = ?R²
?R² = 500
?R = ?500 = 22,36
R = 22,36 x 3,14 = 70,2104 cm²
Não tenho a minima firmeza de que esteja certo, porque nunca fui bem em geometria. Derivadas e integrais são fichinha perto disso.
Peço ajuda urgente, por favor!
Abraços
, onde r é o raio da base. Isto é um dos dados. O que você quer minimizar com material gasto é a área total, que é a soma de todas as áreas do cilindro: 
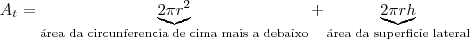
como função de r. Jogue na expressão da área, derive e iguale a zero para encontrar o ponto de mínimo.
