 por PHANIE » Ter Abr 26, 2011 15:53
por PHANIE » Ter Abr 26, 2011 15:53
Num triângulo isósceles, o ângulo  mede 100º . Qual o ângulo formado pelas alturas que não passam pelo vértice A.
resposta : 80 º
eu não to conseguindo fazer as alturas
-
PHANIE
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Mar 30, 2011 15:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: PATOLOGIA
- Andamento: formado
 por FilipeCaceres » Ter Abr 26, 2011 19:52
por FilipeCaceres » Ter Abr 26, 2011 19:52
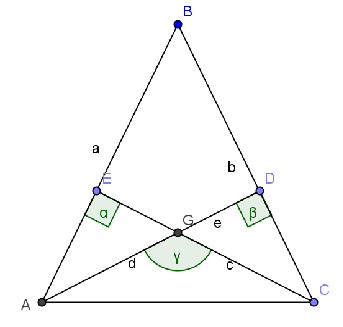
- triangulo.png (11.38 KiB) Exibido 14129 vezes
No desenho

e se deseja descobrir quanto vale

Qualquer dúvida poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por PHANIE » Qua Mai 04, 2011 11:54
por PHANIE » Qua Mai 04, 2011 11:54
vc poderia resolver a questão? eu nao to conseguindo..
-
PHANIE
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Mar 30, 2011 15:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: PATOLOGIA
- Andamento: formado
 por FilipeCaceres » Qua Mai 04, 2011 12:17
por FilipeCaceres » Qua Mai 04, 2011 12:17
Como o triângulo é isósceles, temos que
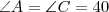
Trançando as alturas, temos 2 triângulos retângulo.
Sendo assim temos,
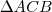
Com


Logo,
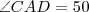
Similarmente para
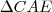
Temos
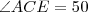
Portanto,

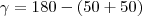
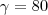
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fuvest-SP
por luanxd » Dom Fev 07, 2010 20:16
- 4 Respostas
- 5412 Exibições
- Última mensagem por luanxd

Ter Fev 09, 2010 11:06
Sistemas de Equações
-
- Fuvest
por CaAtr » Sex Abr 02, 2010 16:39
- 5 Respostas
- 4642 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 14:27
Sistemas de Equações
-
- LOG FUVEST
por PHANIE » Ter Abr 12, 2011 13:22
- 1 Respostas
- 14737 Exibições
- Última mensagem por Molina

Ter Abr 12, 2011 15:13
Logaritmos
-
- fuvest 2
por PHANIE » Ter Abr 26, 2011 15:57
- 3 Respostas
- 5025 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:33
Geometria Plana
-
- fuvest
por karen » Qua Nov 28, 2012 14:48
- 1 Respostas
- 1296 Exibições
- Última mensagem por young_jedi

Qua Nov 28, 2012 16:10
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e se deseja descobrir quanto vale
e se deseja descobrir quanto vale 


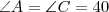
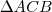


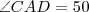
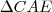
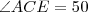

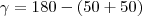
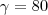


 .
.
 :
: