por PHANIE » Seg Abr 25, 2011 15:20
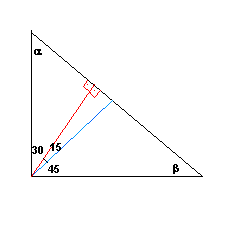
Num triângulo retângulo, a altura relativa à hipotenusa forma com a bissetriz do ângulo reto um ângulo de 15 º . Calcular os ângulos agudos.
resposta: 30 º e 60 º
eu to com dificuldade para fazer o desenho
-
PHANIE
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Qua Mar 30, 2011 15:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: PATOLOGIA
- Andamento: formado
por FilipeCaceres » Seg Abr 25, 2011 20:36
- traingulo2.PNG (2.58 KiB) Exibido 3330 vezes
Em vermelho é a altura.
Em azul é a bissetriz.
Os ângulos
e
é que se deseja encontrar.
Qualquer dúvida poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por LuizAquino » Seg Abr 25, 2011 20:46
DicaPara realizar construções geométricas (e muito mais), eu recomendo o programa GeoGebra. A página oficial do programa é:
http://www.geogebra.orgNo meu canal há uma série de vídeos ensinando a usar esse programa:
http://www.youtube.com/LCMAquino
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Semelhança de triângulos] Triângulos quadrados
por Debora Bruna » Seg Ago 08, 2016 12:18
- 0 Respostas
- 1384 Exibições
- Última mensagem por Debora Bruna
Seg Ago 08, 2016 12:18
Geometria Plana
-
- Triângulos
por claudia » Ter Nov 11, 2008 13:58
- 14 Respostas
- 10330 Exibições
- Última mensagem por claudia
Ter Nov 18, 2008 14:43
Geometria Plana
-
- Triângulos
por Mandu » Dom Out 24, 2010 21:30
- 1 Respostas
- 1459 Exibições
- Última mensagem por Mandu
Dom Out 24, 2010 21:31
Geometria Plana
-
- UEL-PR triângulos
por Kelvin Brayan » Qui Abr 07, 2011 03:00
- 7 Respostas
- 27663 Exibições
- Última mensagem por kamillanjb
Sex Abr 08, 2011 09:36
Geometria Plana
-
- Triângulos
por Ansellmo » Ter Mar 15, 2016 03:09
- 0 Respostas
- 1164 Exibições
- Última mensagem por Ansellmo
Ter Mar 15, 2016 03:09
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
Resposta:
Dica:
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a
e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
