UF-MG- Geometria. Determine a área do polígono

[andersontricordiano]

(U F MG) Na figura ABC é um triângulo retângulo com catetos de medidas BC=3 e BA=4; a circunferência de centro O, inscrita no triângulo, tangencia-o nos pontos D e E. Determine a área do poligono ABEOD

Resposta: 4

triangulo e circulo.jpg (10.5 KiB) Exibido 4941 vezes

Por favor me ajudem a resolver esse calculo!
Obrigado quem me ajudar!!!!

[LuizAquino]

Analise a figura abaixo e responda as perguntas.

triangulo-exercicio-ufmg.png (7.15 KiB) Exibido 4929 vezes

1) Qual a relação que existe entre os triângulos AGO e ADO? E entre os triângulos OEC e ODC?
2) Qual é a medida de AG? E de EC?

[LucasVNPKBS]

Ae você so precisa usar a relação:

Raio= Semiperimetro do triangulo - Lado maior do triagulo

Você vai achar o raio igual a 1, e pronto, na hora de calcular a área fica muito fácil, calcula uma de cada vez, soma tudo e o resultado da igual a 4.

[MarceloFantini]

Recomendaria que você não usasse o resultado que o Lucas mencionou por razões de que isso acaba tornando-se decoreba e se você não sabe resolver sem gerará problemas futuramente.

[profmatematica]

Pois eu seguiria a ideia do Lucas sim pode fazer q sai beleza o exercicio

[MarceloFantini]

Não adiantar sair se não entender porque saiu.

[FilipeCaceres]

triangulo-exercicio-ufmg.GIF (3.78 KiB) Exibido 4882 vezes

Editei a figura do LuizAquino para mostrar uma forma muito simples e rápida, que é usando segmentos tangentes.

Desta forma temos que:




Logo,



Assim temos que a área pedida é:



Espero ter ajudado.

[profmatematica]

Felipe parabens ficou clara logica e precisa sua explicacao

[LuizAquino]

Vejamos como solucionar o exercício usando o caminho que eu havia indicado inicialmente. Nós usaremos Congruência de Triângulos.

1) Qual a relação que existe entre os triângulos AGO e ADO? E entre os triângulos OEC e ODC?

Temos os triângulos retângulos AGO e ADO. Eles possuem a mesma hipotenusa (AO) e um mesmo cateto (GO=OD=r). Portanto, AG=AD. Desse modo, AGO e ADO são congruentes pelo caso LLL.

De modo análogo, OEC e ODC também são congruentes pelo caso LLL.

2) Qual é a medida de AG? E de EC?

Como ilustrou filipecaceres, temos que AG=4-r e EC=3-r.

Agora, após respondido as duas peguntas que eu havia feito, bastava pensar um pouquinho e chegar a conclusão que (4-r)+(3-r)=AC.

Lembrando que ABC é um triângulo retângulo, que AC é a hipotenusa e os catetos são AB=4 e BC=3, teremos que AC=5. A partir daí basta montar a equação (4-r)+(3-r)=5 e continuar a solução como indicou filipecaceres.
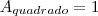
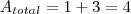