 por idacil » Sáb Fev 26, 2011 17:48
por idacil » Sáb Fev 26, 2011 17:48
Um plano é determinado pelos pontos M, N e P, do cubo representado na figura abaixo, que são pontos médios das arestas GF, AH e BC, respectivamente.

a) Determine a secção desse plano com o cubo.
b) Considere que a medida da aresta do cubo seja a .
Calcule a área dessa secção em função de a .
c) Encontre três pontos (sobre as arestas do cubo) que
determinam um plano que seccione o cubo, em um trapézio
isósceles.
RESPOSTAS:
A)

B)
A/2...???????
C)

?????????????????????????
2) Um sólido de revolução, obtido pela rotação de uma figura F ao redor de um eixo e , resulta em um cone circular reto e um cilindro circular reto, como na ilustração.

a) Determine a posição do eixo na figura ao lado e a área de F em função do raio R, sabendo que as geratrizes do cone e do cilindro medem o triplo de R.
b) Determine o valor de R de modo que a secção por um plano que contenha o eixo e tenha área igual a 12 cm2.
RESPOSTAS:
A) se a região é um triangulo retangulo com base no eixo x e 2 verteces nos ponto (a,0) e (b,0) com angulo reto, então o eixo é vertical.
Area total =

* r (g+r)
Area total = 3,14 * r(3r+r)
Area total = 3,14 * 5r
Area total = 15,70r
b) 12 = 15,70r
12 = r
15,70
r = 0,76
Por favor, me ajudem.
-
idacil
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Fev 04, 2011 14:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Abelardo » Seg Mar 07, 2011 01:58
por Abelardo » Seg Mar 07, 2011 01:58
Sabendo que o triângulo seccionado é equilátero, precisamos determinar o valor de qualquer lado e depois usar a fórmula da área de um triângulo equilátero.
Chamando de x um lado desse triângulo, temos:
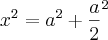
( observe que para determinar o lado NP, ele é a hipotenusa de um triângulo com catetos NA e PA. Logo, nessa equação, procuramos o valor de PA... consegue ver esse triângulo)!
... ..
... ..
... ..
![x=\frac{a \sqrt[] {5}}{4} x=\frac{a \sqrt[] {5}}{4}](/latexrender/pictures/504e470ba67aaee0a941546492a7c0b4.png)
Calculemos agora o valor de NP, temos o valor de NA=
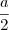
e PA=
![x=\frac{a \sqrt[] {5}}{4} x=\frac{a \sqrt[] {5}}{4}](/latexrender/pictures/504e470ba67aaee0a941546492a7c0b4.png)
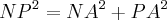
.......
.......
.......
.......
NP=
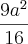
.
Sabendo que a área de um triângulo equilátero é

.
Como temos o valor de um lado, NP.. é só substituir e encontramos no final :
![\frac{9{a}^{2}\sqrt[]{3}}{64} \frac{9{a}^{2}\sqrt[]{3}}{64}](/latexrender/pictures/4d3addd37603cdcacaeee3460349dbd9.png)
. Tá ai a letra B.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana/Espacial
 por Emilia » Ter Fev 22, 2011 15:33
por Emilia » Ter Fev 22, 2011 15:33
- 0 Respostas
- 2133 Exibições
- Última mensagem por Emilia

Ter Fev 22, 2011 15:33
Geometria Plana
-
- GEOMETRIA METRICA E ESPACIAL,TRIGONOMETRIA PLANA
 por solcruz » Sáb Mar 05, 2011 20:54
por solcruz » Sáb Mar 05, 2011 20:54
- 1 Respostas
- 3451 Exibições
- Última mensagem por Abner

Dom Mar 13, 2011 11:35
Trigonometria
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11735 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2847 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6145 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ?????????????????????????
?????????????????????????
 * r (g+r)
* r (g+r)

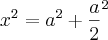 ( observe que para determinar o lado NP, ele é a hipotenusa de um triângulo com catetos NA e PA. Logo, nessa equação, procuramos o valor de PA... consegue ver esse triângulo)!
( observe que para determinar o lado NP, ele é a hipotenusa de um triângulo com catetos NA e PA. Logo, nessa equação, procuramos o valor de PA... consegue ver esse triângulo)!![x=\frac{a \sqrt[] {5}}{4} x=\frac{a \sqrt[] {5}}{4}](/latexrender/pictures/504e470ba67aaee0a941546492a7c0b4.png)
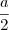 e PA=
e PA=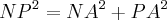
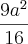 .
. .
.![\frac{9{a}^{2}\sqrt[]{3}}{64} \frac{9{a}^{2}\sqrt[]{3}}{64}](/latexrender/pictures/4d3addd37603cdcacaeee3460349dbd9.png) . Tá ai a letra B.
. Tá ai a letra B.





