 por PedroSantos » Qua Fev 23, 2011 13:26
por PedroSantos » Qua Fev 23, 2011 13:26
Seja a função dada pela expressão
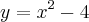
.
É fácil concluir que a concavidade da parabola é virada para cima e que os seus zeros são -2 e 2. Pode-se ainda concluir que as coordenadas do vertice são (0,-4), pois se os zeros são -2 e 2 e a parabola é uma figura com simetria, a abscissa será
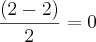
e a ordenada
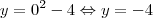
. Conforme se pode verificar na figura:
E as coordenadas do foco e a recta da directriz?Como posso achar estes dados a partir da expressão inicial?
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por Dan » Qua Fev 23, 2011 16:16
por Dan » Qua Fev 23, 2011 16:16
Olá PedroSantos.
Você precisa primeiramente passar a equação para a forma
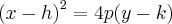
. Pode usar completamento de quadrados, por exemplo.
Depois disso você calcula o foco e a diretriz:
Foco:
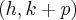
Diretriz:
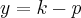
No caso dessa parábola, a equação será

A partir disso você calcula foco e diretriz. Não esqueça que 4p = 1 e que k = -4.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Fev 23, 2011 16:22
por LuizAquino » Qua Fev 23, 2011 16:22
Dos conhecimentos de Geometria Analítica, sabemos que uma parábola de foco F=(0, p) e reta diretriz r : y=-p tem equação igual a

.
Para transformar a sua equação nesse formato, vamos fazer uma translação do sistema de eixos de modo que o novo sistema terá a sua origem no ponto (0, -4) do eixo antigo. Isto é, teremos o novo sistema
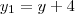
e

. Sendo assim, a equação
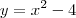
fica equivalente a

no novo sistema.
Nesse novo sistema, temos que o foco será
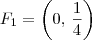
e a reta diretriz será
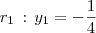
.
Agora, voltando novamente para o sistema de eixos original, teremos que o foco será
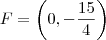
e a reta diretriz será
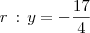
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por PedroSantos » Qua Fev 23, 2011 22:17
por PedroSantos » Qua Fev 23, 2011 22:17
Obrigado pela ajuda, aos dois.A minha dificuldade estava mesmo em colocar a expressão inicial na forma

.
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por PedroSantos » Qui Fev 24, 2011 10:24
por PedroSantos » Qui Fev 24, 2011 10:24
Entretanto estive a verificar outro exemplo.

Aqui é necessário colocar na forma
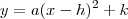
É preciso achar um número que adicionado a

transforme a expressão num trinómio quadrado prefeito. Sabemos que 2ab=5x e que a=x logo b=5/2, assim
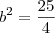
Por isso o trinomio do quadrado perfeito fica
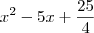
.Agora é necessário adicionar o simétrico do número que utilizamos como artificio.
Fica :
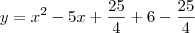
Depois de simplificar a expressão ficamos com
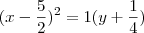
Temos:
h=5/2
k=-1/4
p=1/4
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por LuizAquino » Qui Fev 24, 2011 10:45
por LuizAquino » Qui Fev 24, 2011 10:45
Como você mesmo fez,

pode ser escrita como
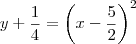
.
Isso significa que o seu novo sistema de eixos deve ser transladado de modo que sua origem seja no ponto
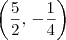
do sistema atual. Isto é, teremos que
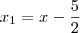
e
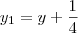
.
Nesse novo sistema, a equação da parábola é

, e portanto o foco é
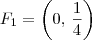
.
Agora, basta transformar esse ponto de volta para o sistema original, obtendo assim
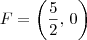
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2856 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- [Parábola] Encontrando o ponto na parábola
por Ana_Rodrigues » Ter Nov 22, 2011 20:44
- 1 Respostas
- 5003 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 21:38
Geometria Analítica
-
- Parábola
por flavio2010 » Sáb Jul 17, 2010 19:11
- 1 Respostas
- 2027 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:20
Funções
-
- Parábola
por flavio2010 » Dom Jul 18, 2010 19:42
- 1 Respostas
- 1919 Exibições
- Última mensagem por Tom

Dom Jul 18, 2010 23:31
Funções
-
- Parábola
por flavio2010 » Sex Jul 23, 2010 19:16
- 1 Respostas
- 2019 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 24, 2010 01:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
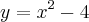 .
.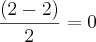 e a ordenada
e a ordenada 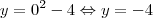 . Conforme se pode verificar na figura:
. Conforme se pode verificar na figura:

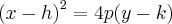 . Pode usar completamento de quadrados, por exemplo.
. Pode usar completamento de quadrados, por exemplo.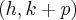
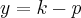


 .
.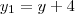 e
e  . Sendo assim, a equação
. Sendo assim, a equação 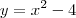 fica equivalente a
fica equivalente a  no novo sistema.
no novo sistema.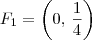 e a reta diretriz será
e a reta diretriz será 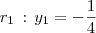 .
.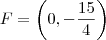 e a reta diretriz será
e a reta diretriz será 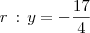 .
.
 .
.
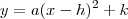
 transforme a expressão num trinómio quadrado prefeito. Sabemos que 2ab=5x e que a=x logo b=5/2, assim
transforme a expressão num trinómio quadrado prefeito. Sabemos que 2ab=5x e que a=x logo b=5/2, assim 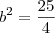
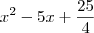 .Agora é necessário adicionar o simétrico do número que utilizamos como artificio.
.Agora é necessário adicionar o simétrico do número que utilizamos como artificio.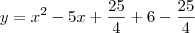
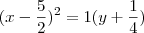
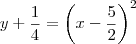 .
.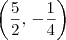 do sistema atual. Isto é, teremos que
do sistema atual. Isto é, teremos que 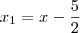 e
e 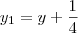 .
. , e portanto o foco é
, e portanto o foco é 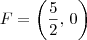 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.