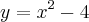 .
.É fácil concluir que a concavidade da parabola é virada para cima e que os seus zeros são -2 e 2. Pode-se ainda concluir que as coordenadas do vertice são (0,-4), pois se os zeros são -2 e 2 e a parabola é uma figura com simetria, a abscissa será
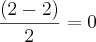 e a ordenada
e a ordenada 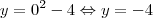 . Conforme se pode verificar na figura:
. Conforme se pode verificar na figura:E as coordenadas do foco e a recta da directriz?Como posso achar estes dados a partir da expressão inicial?


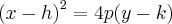 . Pode usar completamento de quadrados, por exemplo.
. Pode usar completamento de quadrados, por exemplo.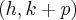
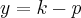


 .
.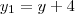 e
e  . Sendo assim, a equação
. Sendo assim, a equação 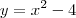 fica equivalente a
fica equivalente a  no novo sistema.
no novo sistema.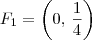 e a reta diretriz será
e a reta diretriz será 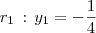 .
.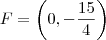 e a reta diretriz será
e a reta diretriz será 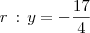 .
.
 .
.
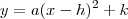
 transforme a expressão num trinómio quadrado prefeito. Sabemos que 2ab=5x e que a=x logo b=5/2, assim
transforme a expressão num trinómio quadrado prefeito. Sabemos que 2ab=5x e que a=x logo b=5/2, assim 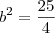
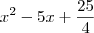 .Agora é necessário adicionar o simétrico do número que utilizamos como artificio.
.Agora é necessário adicionar o simétrico do número que utilizamos como artificio.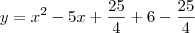
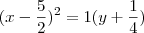
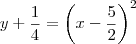 .
.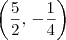 do sistema atual. Isto é, teremos que
do sistema atual. Isto é, teremos que 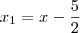 e
e 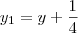 .
. , e portanto o foco é
, e portanto o foco é 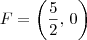 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)