 por von grap » Qui Fev 17, 2011 10:41
por von grap » Qui Fev 17, 2011 10:41
Dá uma ajuda pessoal...
1-No piso de um salão retangular foram usados 1200 tacos quadrados. Em outro salão retangular, cujas dimensões são 20% maiores que as do primeiro, quantos desses tacos devem ser usados?
2-Um retângulo R é tal que seu comprimento é 20% maior do que o lado de um quadrado Q, e sua largura é 20% menor que o lado do mesmo Q. Qual é a razão entre as áreas de R e Q, nessa ordem?
Valeu!!!
-
von grap
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Seg Dez 07, 2009 15:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Qui Fev 17, 2011 17:33
por DanielFerreira » Qui Fev 17, 2011 17:33
1-No piso de um salão retangular foram usados 1200 tacos quadrados. Em outro salão retangular, cujas dimensões são 20% maiores que as do primeiro, quantos desses tacos devem ser usados?
xy = 1200
![[x + \frac{20x}{100}][y + \frac{20y}{100}] = [\frac{120x}{100}][\frac{120y}{100}] = \frac{144xy}{100} [x + \frac{20x}{100}][y + \frac{20y}{100}] = [\frac{120x}{100}][\frac{120y}{100}] = \frac{144xy}{100}](/latexrender/pictures/4fc5b58e5ea00dc13eda6c01b7c67146.png)
por regra de três...
xy --------------------------------- 1200

-------------------------- k


"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qui Fev 17, 2011 17:42
por DanielFerreira » Qui Fev 17, 2011 17:42
2-Um retângulo R é tal que seu comprimento é 20% maior do que o lado de um quadrado Q, e sua largura é 20% menor que o lado do mesmo Q. Qual é a razão entre as áreas de R e Q, nessa ordem?
Quadradolado = l
Retângulocomprimento: l +
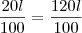
largura: l -

S =

S = l²
Então,
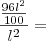
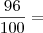

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8717 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4697 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4813 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2533 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3665 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![[x + \frac{20x}{100}][y + \frac{20y}{100}] = [\frac{120x}{100}][\frac{120y}{100}] = \frac{144xy}{100} [x + \frac{20x}{100}][y + \frac{20y}{100}] = [\frac{120x}{100}][\frac{120y}{100}] = \frac{144xy}{100}](/latexrender/pictures/4fc5b58e5ea00dc13eda6c01b7c67146.png)
 -------------------------- k
-------------------------- k


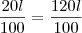


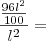
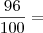

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)