O outro cateto mede 3,75cm . calcule os lados desconhecidos. R:6,25 e 5 cm
bom eu tentei fazer de tal maneira



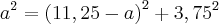
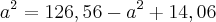

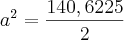
![a=\sqrt[]{70,31} a=\sqrt[]{70,31}](/latexrender/pictures/d80d48849750f2ca96e5eec4ed28e6f5.png)

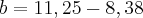
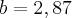
O que nao é a resposta certa , mas eu nao encontrei outra maneire de fazer este .
ajuda por favor .
Detalhe , eu tirei a raiz na calculadora o q é péssimo


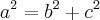 --> Teorema de Pitágoras
--> Teorema de Pitágoras




